Language Safety Score, revisited
08 Aug 2015A couple of weeks ago, I came across this blog post by Steve Shogren, which looks at various programming languages, and attempts to define a “language safety score”, by taking into account a list of language criteria (Are nulls allowed? Can variables be mutated? And so on), aggregating them into an overall safety score – and finally looking for whether the resulting score was a reasonable predictor for the observed bug rate across various projects.
I thought this was an interesting idea. However, I also had reservations on the methodology. Picking a somewhat arbitrary list of criteria, giving them indiscriminately the same weight, and summing them up, didn’t seem to me like the most effective approach – especially given that Steve had already collected a nice dataset. If the goal is to identify which language features best predict how buggy the code will be, why not start from there, and build a model which attempts to predict the bug rate based on language features?
So I decided to give it a shot, and build a quick-and-dirty logistic regression model. In a nutshell, logistic regression attempts to model the probability of observing an event, based on a set of criteria / features. A prototypical application would be in medicine, trying to predict, for instance, the chances of developing a disease, given patient characteristics. In our case, the disease is a bug, and the patient a code base. We’ll use the criteria listed by Steve as potential predictors, and, as a nice side-product of logistic regression, we will get a quantification of how important each of the criteria is in predicting the bug rate.
I’ll discuss later some potential issues with the approach; for now, let’s build a model, and see where that leads us. I lifted the data from Steve’s post (hopefully without typos), with one minor modification: instead of scoring criteria as 1, 0 or –1, I just retained 1 or 0 (it’s there or it’s not there), and prepared an F# script, using the Accord framework to run my logistic regression.
Note: the entire script is here as a Gist.
#I @"../packages"
#r @"Accord.3.0.1-alpha\lib\net45\Accord.dll"
#r @"Accord.MachineLearning.3.0.1-alpha\lib\net45\Accord.MachineLearning.dll"
#r @"Accord.Math.3.0.1-alpha\lib\net45\Accord.Math.dll"
#r @"Accord.Statistics.3.0.1-alpha\lib\net45\Accord.Statistics.dll"
let language, bugrate, criteria =
[|"F#", 0.023486288,[|1.;1.;1.;0.;1.;1.;1.;0.;0.;0.;1.;1.;1.;0.|]
"Haskell", 0.015551204,[|1.;1.;1.;0.;1.;1.;1.;1.;1.;0.;1.;1.;0.;1.|]
"Javascript", 0.039445132,[|0.;0.;0.;0.;0.;0.;0.;0.;0.;0.;1.;0.;1.;0.|]
"CoffeeScript", 0.047242288,[|0.;0.;0.;0.;0.;0.;0.;0.;0.;0.;1.;0.;1.;0.|]
"Clojure", 0.011503478,[|0.;1.;0.;0.;0.;0.;1.;0.;1.;1.;1.;0.;0.;0.|]
"C#", 0.03261284, [|0.;0.;1.;0.;0.;1.;1.;0.;0.;0.;1.;0.;1.;0.|]
"Python", 0.02531419, [|0.;0.;0.;0.;0.;0.;0.;0.;0.;0.;1.;0.;1.;0.|]
"Java", 0.032567736,[|0.;0.;0.;0.;0.;0.;0.;0.;0.;0.;1.;0.;1.;0.|]
"Ruby", 0.020303702,[|0.;0.;0.;0.;0.;0.;0.;0.;0.;0.;1.;0.;1.;0.|]
"Scala", 0.01904762, [|1.;1.;1.;0.;1.;1.;1.;0.;0.;0.;1.;0.;0.;0.|]
"Go", 0.024698375,[|0.;0.;1.;0.;0.;1.;1.;0.;0.;0.;1.;0.;1.;0.|]
"PHP", 0.031669293,[|0.;0.;0.;0.;0.;0.;0.;0.;0.;0.;1.;0.;1.;0.|] |]
|> Array.unzip3
open Accord.Statistics.Models.Regression
open Accord.Statistics.Models.Regression.Fitting
let features = 14
let model = LogisticRegression(features)
let learner = LogisticGradientDescent(model)
let rec learn () =
let delta = learner.Run(criteria, bugrate)
if delta > 0.0001
then learn ()
else ignore ()
learn () |> ignore
And we are done – we have trained a model to predict the bug rate, based on our 14 criteria. How is this working? Let’s find out:
for i in 0 .. (language.Length - 1) do
let lang = language.[i]
let predicted = model.Compute(criteria.[i])
let real = bugrate.[i]
printfn "%16s Real: %.3f Pred: %.3f" lang real predicted
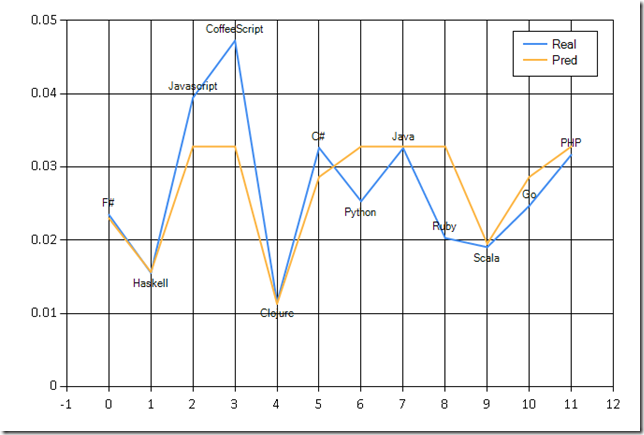
>
F# Real: 0.023 Pred: 0.023
Haskell Real: 0.016 Pred: 0.016
Javascript Real: 0.039 Pred: 0.033
CoffeeScript Real: 0.047 Pred: 0.033
Clojure Real: 0.012 Pred: 0.011
C# Real: 0.033 Pred: 0.029
Python Real: 0.025 Pred: 0.033
Java Real: 0.033 Pred: 0.033
Ruby Real: 0.020 Pred: 0.033
Scala Real: 0.019 Pred: 0.020
Go Real: 0.025 Pred: 0.029
PHP Real: 0.032 Pred: 0.033
Looks pretty good. Let’s confirm that with a chart, using FSharp.Charting:
#load "FSharp.Charting.0.90.12\FSharp.Charting.fsx"
open FSharp.Charting
let last = language.Length - 1
Chart.Combine [
Chart.Line ([ for i in 0 .. last -> bugrate.[i]], "Real", Labels=language)
Chart.Line ([ for i in 0 .. last -> model.Compute(criteria.[i])], "Pred") ]
|> Chart.WithLegend()
What criteria did our model identify as predictors for bugs? Let’s find out.
let criteriaNames = [|
"Null Variable Usage"
"Null List Iteration"
"Prevent Variable Reuse"
"Ensure List Element Exists"
"Safe Type Casting"
"Passing Wrong Type"
"Misspelled Method"
"Missing Enum Value"
"Variable Mutation"
"Prevent Deadlocks"
"Memory Deallocation"
"Tail Call Optimization"
"Guaranteed Code Evaluation"
"Functional Purity" |]
for i in 0 .. (features - 1) do
let name = criteriaNames.[i]
let wald = model.GetWaldTest(i)
let odds = model.GetOddsRatio(i)
(printfn "%28s odds: %4.2f significant: %b" name odds wald.Significant)
>
Null Variable Usage odds: 0.22 significant: true
Null List Iteration odds: 0.86 significant: true
Prevent Variable Reuse odds: 0.64 significant: true
Ensure List Element Exists odds: 1.05 significant: true
Safe Type Casting odds: 1.00 significant: false
Passing Wrong Type odds: 0.86 significant: true
Misspelled Method odds: 1.05 significant: true
Missing Enum Value odds: 0.78 significant: true
Variable Mutation odds: 0.86 significant: true
Prevent Deadlocks odds: 0.64 significant: true
Memory Deallocation odds: 0.74 significant: true
Tail Call Optimization odds: 0.22 significant: true
Guaranteed Code Evaluation odds: 1.71 significant: true
Functional Purity odds: 0.69 significant: true
How should you read this? The first output, the odds ratio, describes how much more likely it is to observe success than failure when that criterion is active. In our case, success means “having a bug”, so for instance, if your language prevents using nulls, you’d expect 1.0 / 0.22 = 4.5 times less chances to write bugs. In other words, if the odds are close to 1.0, the criterion doesn’t make much of a difference. The closer to zero it is, the lower the predicted bug count, and vice-versa.
Conclusions and caveats
The 3 most significant predictors of a low bug rate are, in order, no nulls, tail calls optimization, and (to a much lesser degree) lazy evaluation. After that, we have honorable scores for avoiding variable reuse, preventing deadlocks, and functional purity.
So… what’s the bottom line? First off, just based on the bug rates alone, it seems that using functional languages would be a safer bet than Javascript (and CoffeeScript) to avoid bugs.
Then, now would be a good time to reiterate that this is a quick-and-dirty analysis. Specifically, there are some clear issues with the dataset. First, we are fitting 12 languages on 14 criteria – that’s not much to go on. On top of that, there is some data redundancy. None of the languages in our sample has “ensure list element exists” (4th column is filled with zeroes), and all of them guarantee memory de-allocation (11th column filled with ones). I suspect there is some additional redundancy, because of the similarity between the columns.
Note: another interesting discussion would be whether the selected criteria properly cover the differences between languages. I chose to not go into that, and focus strictly on using the data as-is.
I ran the model again, dropping the 2 columns that contain no information; while this doesn’t change the predictions of the model, it does impact a bit the weight of each criterion. The results, while similar, do show some differences:
("Null Variable Usage", 0.0743885639)
("Functional Purity", 0.4565632287)
("Prevent Variable Reuse", 0.5367456237)
("Prevent Deadlocks", 0.5374379877)
("Tail Call Optimization", 0.7028982809)
("Missing Enum Value", 0.7539575884)
("Null List Iteration", 0.7636177784)
("Passing Wrong Type", 0.7636177784)
("Variable Mutation", 0.7646027916)
("Safe Type Casting", 1.072641105)
("Misspelled Method", 1.072641105)
("Guaranteed Code Evaluation", 2.518831684)
Another piece of information I didn’t use is how many commits were taken into consideration. This matters, because the information gathered for PHP is across 10 times more commits than F#, for instance. It wouldn’t be very hard to do – instead of regressing against the bug rate, we could count the clean and buggy commits per language, and proceed along the lines of the last example described here.
In spite of these issues, I think this constitutes a better base to construct a language score index. Rather than picking criteria by hand and giving them arbitrary weights, let the data speak. Measure how well each of them explains defects, and use that as a basis to determine their relative importance.
That’s it for today! Big thanks to Steve Shogren for a stimulating post, and for making the data available. And again, you can find the script here as a Gist.
