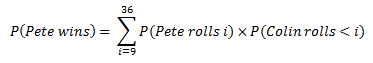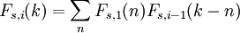Euler Problem 205
09 Aug 2009Today I came across a solution to Euler Problem 205 on The Daily Dose of Excel. The problem is stated as follows:
Peter has nine four-sided (pyramidal) dice, each with faces numbered 1, 2, 3, 4. Colin has six six-sided (cubic) dice, each with faces numbered 1, 2, 3, 4, 5, 6. Peter and Colin roll their dice and compare totals: the highest total wins. The result is a draw if the totals are equal.
What is the probability that Pyramidal Pete beats Cubic Colin? Give your answer rounded to seven decimal places in the form 0.abcdefg
I thought it was a pretty cool problem; I love probability problems, and had never come across something similar, so it piqued my interest. The solution presented in The Daily Dose was essentially a pretty efficient brute-force enumeration, and I wondered if it was possible to go a bit faster that 6 minutes follow a different approach – using my language of predilection, C#.
[Edited August 9. Note to self: before commenting on other people’s blog posts, I should make sure I read them properly. Especially when discussing their code’s performance. Otherwise, I will look foolish].
The probability that Pete wins can be written as:
Refreshing a bit my memory in probability through Wikipedia, “the exact probability distribution Fs,i of a sum of i s-sided dice can be calculated as the repeated convolution of the single-die probability distribution with itself” as follows:
This is already in recursive form, so let’s implement a function which gives us the probability distribution of getting each possibly value throwing i times a s-sided dice:
public class DiceSum
{
public Dictionary<int, double> ComputeDistribution(int sides, int throws)
{
if (throws == 1)
{
var distribution = new Dictionary<int, double>();
for (int outcome = 1; outcome <= sides; outcome++)
{
double probability = 1d / (double)sides;
distribution.Add(outcome, probability);
}
return distribution;
}
else
{
var oneLessThrowDistribution = ComputeDistribution( sides, throws-1);
var oneThrowDistribution = ComputeDistribution(sides, 1);
var distribution = new Dictionary<int, double>();
for (int outcome = throws; outcome <= sides*throws; outcome++)
{
double probability = 0d;
for (int newThrowOutcome = 1; newThrowOutcome <= sides; newThrowOutcome++)
{
if (outcome - newThrowOutcome <= (throws - 1) * sides && outcome - newThrowOutcome >= (throws-1))
{
probability += oneThrowDistribution[newThrowOutcome] * oneLessThrowDistribution[outcome - newThrowOutcome];
}
}
distribution.Add(outcome, probability);
}
return distribution;
}
}
}
We can now write the probability to win for any combination of dices and throws:
public class ComputeProbabilityToWin
{
public double Run(int firstSides, int firstThrows, int secondSides, int secondThrows)
{
var diceSum = new DiceSum();
var firstDistribution = diceSum.ComputeDistribution(firstSides, firstThrows);
var secondDistribution = diceSum.ComputeDistribution(secondSides, secondThrows);
var probabilityToWin = 0d;
foreach (int firstThrow in firstDistribution.Keys)
{
double probabilityOfThrow = firstDistribution[firstThrow];
double probabilityToWinThrow = 0d;
foreach (int secondTrow in secondDistribution.Keys)
{
if (secondTrow < firstThrow)
{
probabilityToWinThrow += secondDistribution[secondTrow];
}
}
probabilityToWin += probabilityOfThrow * probabilityToWinThrow;
}
return probabilityToWin;
}
}
And we can run this
static void Main(string[] args)
{
var startTime = DateTime.Now;
Console.Write("Starting computation at " + startTime.ToLongTimeString());
Console.WriteLine(Environment.NewLine);
var compute = new ComputeProbabilityToWin();
double probability = compute.Run(4, 9, 6, 6);
var endTime = DateTime.Now;
Console.WriteLine("Finished computation at " + endTime.ToLongTimeString());
Console.WriteLine(probability);
Console.ReadLine();
}
This runs in under a second. My only worry is that by computing multiple distributions, I am introducing rounding errors, an issue which is less likely with the brute-force enumeration. Modifying the recursive computation to count the cases, and not the probability, should solve that if need be.
My experience has been that usually C# outperforms VBA for calculations, so I can’t directly compare the two approaches; maybe I’ll implement Michael’s solution in C# too, for comparison – but as both solutions run under a second, I might just leave it at that and be lazy… In any case, thanks to Michael for getting this interesting problem to my attention!