The Bee Colony in action
22 May 2011In our previous installments, we laid the groundwork of our Bee Colony Algorithm implementation. Today, it’s time to put the bees to work, searching for an acceptable solution to the Traveling Salesman problem.
We will approach the search as a Sequence: starting from an initial hive and solution, we will unfold it, updating the state of the hive and the current best solution at each step. Let’s start with the hive initialization. Starting from an initial route, we need to create a pre-defined number of each Bee type, and provide them with an initial destination:
let Initialize nScouts nActives nInactives cities (rng : Random) =
[
for i in 1 .. nScouts do
let solution = Evaluate(Shuffle rng cities)
yield Scout(solution)
for i in 1 .. nActives do
let solution = Evaluate(Shuffle rng cities)
yield Active(solution, 0)
for i in 1 .. nActives do
let solution = Evaluate(Shuffle rng cities)
yield Inactive(solution)
]
There is probably a more elegant way to do this, but this is good enough: we use a simple List comprehension to generate a list on the fly, yielding the appropriate number of each type of bees, and assigning them a shuffled version of the starting route.
Next, we need a function to update our hive, and the current best solution available:
let Update (hive, currentBest : Solution) rng =
let searchResult = List.map (fun b -> Search b rng) hive
let newSolutions = List.choose (fun e -> snd e) searchResult
let newBest = List.fold (fun best solution ->
if best.Cost < solution.Cost
then best
else solution) currentBest newSolutions
let inactives = CountInactives hive
let updatedHive = searchResult
|> List.map (fun b -> Waggle newSolutions (fst b) rng)
|> Activate rng inactives
(updatedHive, newBest)
The function takes 2 arguments: a Tuple of the current state of affairs (the hive and the best solution), and a random number generator. First, we use List.map, to apply the Search function we defined earlier to each bee, returning a new List of Tuples, containing each bee and an option containing the result of its search (a new solution, or None). We then extract the new solutions from that list, using List.choose to retrieve the second element of the Tuples when they are not None, and use a List.fold to find the new best solution from that list, if it is better than the current best solution. Finally, we update the Hive, by having each Bee perform its Waggle dance and share its new information via List.map, and applying the Activate function to promote some of the inactive bees to Active status – and return a Tuple of the updated hive and updated best solution.
We are now almost done – we can now define a Solve function, which will call Initialize to create an initial hive, and unfold an infinite Sequence of solutions:
let Solve scouts actives inactives route =
let rng = new Random()
let hive = Initialize scouts actives inactives route rng
let initialBest = List.map (fun b -> Solution b) hive
|> List.minBy (fun s -> s.Cost)
Seq.unfold (fun h -> Some(h, (Update h rng))) (hive, initialBest)
It’s now time to see this in action. Let’s add a file to our project, and create a small console application Program.fs. First, we need a good test case: let’s generate a list of cities named A to Z, located on a circle:
let RandomRoute radius points =
[
let rng = new Random()
let letters = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
for i in 0 .. (points - 1) do
let angle = Math.PI * 2.0 * (double)i / (double)points
let name = letters.[i];
yield {
Solver.City.Name = (string)name;
Solver.City.X = Math.Cos(angle) * radius;
Solver.City.Y = Math.Sin(angle) * radius }
]
If our algorithm is working, it should return a list of cities sorted in alphabetical (or reverse-alphabetical) order.
Next, let’s create an entry point for our console application, and watch the bees at work:
[<EntryPoint>]
let main (args : string[]) =
printfn "Bee Hive colony at work!"
let stopwatch = new Stopwatch()
stopwatch.Start()
let rng = new Random()
let route = RandomRoute 100.0 26
let bestSolution = Solver.Evaluate route
printfn "Best possible cost: %f" bestSolution.Cost
let initialSolution = Solver.Evaluate (Solver.Shuffle rng route)
printfn "Initial cost: %f " initialSolution.Cost
let search = Solver.Solve 30 50 20 route
let solution = search |> Seq.nth 20000 |> snd
stopwatch.Stop()
printfn "Milliseconds: %d" stopwatch.ElapsedMilliseconds
printfn "Solution cost: %f" solution.Cost
solution.Route |> List.iter (fun c -> printf "%s " c.Name)
printfn ""
printfn "Press enter to close"
Console.ReadLine() |> ignore
0
Running this produces the following:
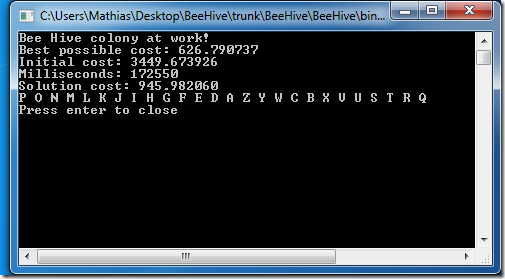
In about three minutes, starting from a path of length 3450, we found a solution of length 946, out of a possible best of 627. The list has long stretches of correctly reverse-sorted cities (it got D to R properly ordered), with a few misplaced cities. Not too bad!
Before going further, here is the complete code I wrote so far, in its current state. First, the Solver.fs file, which contains the algorithm logic:
module Solver
open System
let probaFalsePositive = 0.1 // proba to incorrectly pick a worse solution
let probaFalseNegative = 0.1 // proba to miss an improved solution
let tripsLimit = 100 // number of trips without improvements a bee can make
let probaConvince = 0.8 // proba to convince a bee to target a better solution
let SwapIndexPairs (rng : Random) list =
seq {
for i in (List.length list - 1) .. -1 .. 1 do
yield (i, rng.Next(i + 1)) }
let SwapIndexMap index (moveIndex, toIndex) =
if index = moveIndex then toIndex
elif index = toIndex then moveIndex
else index
let Swap indexPair list =
let length = List.length list
List.permute (fun index -> SwapIndexMap index indexPair) list
let Shuffle (rng : Random) list =
let length = List.length list
let indexPairs = SwapIndexPairs rng list
Seq.scan (fun currentList indexPair -> Swap indexPair currentList)
list indexPairs
|> Seq.nth (length - 1)
let SwapWithNextIndexMap index swapIndex length =
let flipWith = (swapIndex + 1) % length
SwapIndexMap index (swapIndex, flipWith)
let SwapWithNext swapIndex list =
let length = List.length list
List.permute (fun index -> SwapWithNextIndexMap index swapIndex length) list
let SwapRandomNeighbors list =
let random = new Random()
let index = random.Next(0, List.length list)
SwapWithNext index list
type City = { Name: string; X: float; Y: float; }
let Distance (city1, city2) =
((city1.X - city2.X) ** 2.0
+ (city1.Y - city2.Y) ** 2.0) ** 0.5
let CircuitCost list =
seq {
for i in 0 .. (List.length list - 1) -> list.[i]
yield List.head list
}
|> Seq.pairwise
|> Seq.map Distance
|> Seq.sum
type Solution = { Route: List<City>; Cost: float }
let Evaluate (route: List<City>) = { Route = route; Cost = CircuitCost route }
type Bee =
| Scout of Solution
| Active of Solution * int
| Inactive of Solution
let Search bee (rng : Random) =
match bee with
| Scout solution ->
let newSolution = Evaluate (Shuffle rng solution.Route)
if newSolution.Cost < solution.Cost
then (Scout(newSolution), Some(newSolution))
else (bee, None)
| Active (solution, visits) ->
let newSolution = Evaluate (SwapRandomNeighbors solution.Route)
let proba = rng.NextDouble()
if newSolution.Cost < solution.Cost
then
if proba < probaFalseNegative
then (Active(solution, (visits + 1)), None)
else (Active(newSolution, 0), Some(newSolution))
else
if proba < probaFalsePositive
then (Active(newSolution, 0), Some(newSolution))
else (Active(solution, (visits + 1)), None)
| Inactive solution -> (bee, None)
let Solution bee =
match bee with
| Scout(solution) -> solution
| Inactive(solution) -> solution
| Active(solution, trips) -> solution
let (|RequiresUpdate|) bee =
match bee with
| Scout(solution) -> false
| Inactive(solution) -> true
| Active(solution, trips) -> trips > tripsLimit
let Waggle (solutions : List<Solution>) (bee : Bee) (rng : Random) =
match bee with
| RequiresUpdate true ->
let currentSolution = Solution bee
let newSolution = List.fold (fun acc element ->
if element.Cost < acc.Cost && rng.NextDouble() < probaConvince
then element else acc) currentSolution solutions
Inactive(newSolution)
| _ -> bee
let Promote bee =
match bee with
| Inactive(solution) -> Active(solution, 0)
| _ -> bee
let Activate rng inactives bees =
let inactiveIndexes =
List.mapi (fun i b -> match b with
| Inactive(solution) -> Some(i)
| _ -> None)
bees
|> List.choose (fun e -> e)
|> Shuffle rng
let promoted = (List.length inactiveIndexes) - inactives
let promotedIndexes = Seq.take promoted inactiveIndexes |> Seq.toList
bees |> List.mapi (
fun i b -> if List.exists (fun e -> e = i) promotedIndexes
then Promote b
else b)
let CountInactives hive =
hive |> List.choose (fun b -> match b with
| Inactive(solution) -> Some(b)
| _ -> None)
|> List.length
let Initialize nScouts nActives nInactives cities (rng : Random) =
[
for i in 1 .. nScouts do
let solution = Evaluate(Shuffle rng cities)
yield Scout(solution)
for i in 1 .. nActives do
let solution = Evaluate(Shuffle rng cities)
yield Active(solution, 0)
for i in 1 .. nActives do
let solution = Evaluate(Shuffle rng cities)
yield Inactive(solution)
]
let Update (hive, currentBest : Solution) rng =
let searchResult = List.map (fun b -> Search b rng) hive
let newSolutions = List.choose (fun e -> snd e) searchResult
let newBest = List.fold (fun best solution ->
if best.Cost < solution.Cost
then best
else solution) currentBest newSolutions
let inactives = CountInactives hive
let updatedHive = searchResult
|> List.map (fun b -> Waggle newSolutions (fst b) rng)
|> Activate rng inactives
(updatedHive, newBest)
let Solve scouts actives inactives route =
let rng = new Random()
let hive = Initialize scouts actives inactives route rng
let initialBest = List.map (fun b -> Solution b) hive
|> List.minBy (fun s -> s.Cost)
Seq.unfold (fun h -> Some(h, (Update h rng))) (hive, initialBest)
Then, the Program.fs file, which contains the Console application:
module Program
open System
open System.Diagnostics
let RandomRoute radius points =
[
let rng = new Random()
let letters = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
for i in 0 .. (points - 1) do
let angle = Math.PI * 2.0 * (double)i / (double)points
let name = letters.[i];
yield {
Solver.City.Name = (string)name;
Solver.City.X = Math.Cos(angle) * radius;
Solver.City.Y = Math.Sin(angle) * radius }
]
[<EntryPoint>]
let main (args : string[]) =
printfn "Bee Hive colony at work!"
let stopwatch = new Stopwatch()
stopwatch.Start()
let rng = new Random()
let route = RandomRoute 100.0 26
let bestSolution = Solver.Evaluate route
printfn "Best possible cost: %f" bestSolution.Cost
let initialSolution = Solver.Evaluate (Solver.Shuffle rng route)
printfn "Initial cost: %f " initialSolution.Cost
let search = Solver.Solve 30 50 20 route
let solution = search |> Seq.nth 20000 |> snd
stopwatch.Stop()
printfn "Milliseconds: %d" stopwatch.ElapsedMilliseconds
printfn "Solution cost: %f" solution.Cost
solution.Route |> List.iter (fun c -> printf "%s " c.Name)
printfn ""
printfn "Press enter to close"
Console.ReadLine() |> ignore
0
At that stage, we have a running algorithm, which seems to be doing what we expect, in about 200 lines of code. I am sure that code could be improved, and I would love to hear comments or suggestions to make it better!
My next objective will be to parallelize that code, to make it hopefully faster. Most of the code should be suitable for this, because we are operating on immutable structures, except for one issue, the random number generator, which uses the non-thread-safe Random() class. Stay tuned!
