Create optimization programs dynamically with C# and the Microsoft Solver Foundation

In our last post, we explored how the Microsoft Solver Foundation can be used to solve simple maximization/minimization problems from C#. The problem we looked at is the following: given a set of products, each with a unit cost, a reselling price, and a weight, how can we maximize profit if we have only a limited budget and a limited weight capacity available.

Expressing and resolving the problem for a particular set of inputs was rather easy. However, the example we presented was very static: the decisions, the goal and the constraints were completely hard-coded.

The real value I found in the Microsoft Solver Foundation is that it can be completely integrated in your .NET code, working with strongly-typed objects. Today, we will revisit the same example we presented previously, but our goal will be to make the optimization program “generic”, so that we can resolve the same prototypical problem, given any set of inputs.

At a high level, what we are looking for is a class which, given a collection of Products, a Budget and a Capacity, returns a “recommended” purchase quantity for each product, maximizing our profit:

public class Profit
{
   public static IDictionary<Product, int> Maximize(
      IEnumerable<Product> products, 
      double budget, 
      double capacity)
   {
      // do stuff here
   }
}

Let’s first define what a Product is:

public class Product
{
   public Product(string name, double cost, double price, double weight)
   {
      this.Name = name;
      this.Cost = cost;
      this.Price = price;
      this.Weight = weight;
   }

   public string Name { get; private set; }
   public double Cost { get; private set; }
   public double Price { get; private set; }
   public double Weight { get; private set; }
   public double Margin
   {
      get { return this.Price - this.Cost; }
   }
}

Now let’s flesh out the Maximize method. We still need to instantiate a solver and create a model, but, instead of manually creating each decision variables, we want to create one variable per product:

var solver = SolverContext.GetContext();
solver.ClearModel();
var model = solver.CreateModel();

var decisions = products.Select(
   it => new Decision(Domain.IntegerNonnegative, it.Name));
model.AddDecisions(decisions.ToArray());

A few comments here. First, note the solver.ClearModel() line, which has been added to flush out data from other models that might have been run before. This line is necessary, because the SolverContext is a singleton (as far as I can tell). Then, we use the Model.AddDecisions(…) method, which takes in an array of decisions, instead of adding them one by one. Note also that the names of the products are expected to be unique.

So far, so good. The next step, expressing the goal, is trickier. In our previous example, we simply typed in a mathematical expression, relying on the solver to make sense of it. Here, rather than attempting to manually create a string for that expression, we will leverage the SumTermBuilder helper class:

var objective = new SumTermBuilder(decisions.Count());
foreach (var product in products)
{
   var productDecision = model.Decisions.First(
      it => it.Name == product.Name);
   objective.Add(productDecision * product.Margin);
}
model.AddGoal("Profit", GoalKind.Maximize, objective.ToTerm());

What is happening here? If you recall, our objective is to Maximize our Profit, which corresponds to the sum of the profit on each individual product, that is, its Margin multiplied by the Quantity purchased, which happens to be the Decision assigned to each product.

The SumTermBuilder does just that: we iterate over the products, retrieving the decision by matching it with its name, and add to the builder the expression for the Product Profit – and finally pass the Term generated by the SumTermBuilder to our Model.

The Budget and Capacity constraints are handled much in the same way:

var budgetComponents = new SumTermBuilder(decisions.Count());
foreach (var product in products)
{
   var productDecision = model.Decisions.First(
      it => it.Name == product.Name);
   budgetComponents.Add(productDecision * product.Cost);
}

var budgetConstraint = budgetComponents.ToTerm() <= budget;
model.AddConstraint("Budget", budgetConstraint);

var weightComponents = new SumTermBuilder(decisions.Count());
foreach (var product in products)
{
   var productDecision = model.Decisions.First(
      it => it.Name == product.Name);
   weightComponents.Add(productDecision * product.Weight);
}

var weightConstraint = weightComponents.ToTerm() <= capacity;
model.AddConstraint("Weight", weightConstraint);

The only difference with the Goal is that we need to define the type of constraint, in this case, inequality: the cost and the weight of our delivery need to be less or equal than the capacity and the budget. Again, note the fluidity of the syntax in interpreting the inputs.

We have the goal, the decision variables, and the constraints – we are now ready to solve. Let’s do it:

var solution = solver.Solve();

var orders = new Dictionary<Product, int>();
if (solution.Quality == SolverQuality.Optimal)
{
   foreach (var product in products)
   {
      var productDecision = model.Decisions.First(it => it.Name == product.Name);
      orders.Add(product, (int)productDecision.ToDouble());
   }
}

return orders;

I don’t think I need to comment on the solver.Solve() call. Once the solver worked its magic, we check the Quality of the solution, and retrieve the value of each Decision variable from the Model, by calling ToDouble(). Note that decision variables will always be doubles; however, because we stated that the domain of the Decisions was Integers, we know we can safely cast that value to an integer.

Let’s try it out on an example via a Console App:

static void Main(string[] args)
{
   var random = new Random();
   var products = new List<Product>();
   for (var i = 0; i < 100; i++)
   {
      var product = new Product(
         "Name" + i.ToString(),
         10d*random.NextDouble(),
         20d*random.NextDouble(),
         50d*random.NextDouble());
      products.Add(product);
   }

   var clock = new Stopwatch();
   clock.Start();
   var solution = Profit.Maximize(products, 500d, 1000d);
   clock.Stop();
   Console.WriteLine("Time (ms): " + clock.ElapsedMilliseconds);
   foreach (var product in solution)
   {
      if (product.Value > 0)
      {
         Console.WriteLine(product.Key.Name + ": " + product.Value);
      }
   }

   Console.ReadLine();
}

Instead of the 3 products in our original example, we create a set of 100 random Products, and run them through the Solver. The result looks like this:

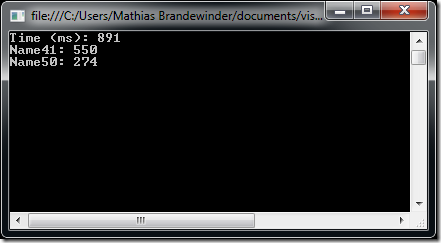
In under a second, the Solver identified an Optimal solution. I say, not bad. As a lower bound approximation, if you simplified the problem and considered the question “should I pick one or zero units of product X”, across 100 products, that would generate 2 ^ 100 combinations, or, if I am to trust Wolfram Alpha, 1.267x10^30 combinations, a 31 decimal digits number – clearly not something you want to enumerate and iterate over.

This is where we’ll stop for today. While the example we used was rather contrived, you could probably imagine how such a selection problem could arise in a business application – for instance, selecting which supplier to ship from, or what stocks should go in a portfolio. What I hoped to illustrate is how the Microsoft Solver Foundation can help you solve complex mathematical optimization problems with limited effort, while integrating fairly smoothly inside your .NET code, using strongly-typed objects, and spare you having to re-invent the wheel and writing custom algorithms which are prone to error.

As usual, I am interested in any comments or questions you might have!