Bipartite matching with Bumblebee
01 Apr 2012Last week’s StackOverflow newsletter contained a fun problem I had never seen before: Bipartite Matching. Here is the problem:
There are N starting points (purple) and N target points (green) in 2D. I want an algorithm that connects starting points to target points by a line segment (brown) without any of these segments intersecting (red) and while minimizing the cumulative length of all segments.
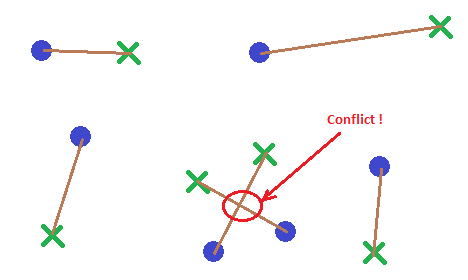Image from the original post on StackOverflow
I figured it would be fun to try out Bumblebee, my artificial bee colony library, on the problem. As the accepted answer points out, the constraint that no segment should intersect is redundant, and we only need to worry about minimizing the cumulative length, because reducing the length implies removing intersections.
As usual with Bumblebee, I’ll go first with the dumbest thing that could work. The solution involves matching points from two lists, so we’ll define a record type for Point and represent a Solution as two (ordered) lists of points, packed in a Tuple:
type Point = { X: float; Y: float }
let points = 100
let firstList = [ for i in 0 .. points -> { X = (float)i ; Y = float(i) } ]
let secondList = [ for i in 0 .. points -> { X = (float)i ; Y = float(i) } ]
let root = firstList, secondList
We’ll start with a silly problem, where the 2 lists are identical: the trivial solution here is to match each point with itself, resulting in a zero-length, which will be convenient to see how well the algorithm is doing and how far it is from the optimum.
How can we Evaluate the quality of a solution? We need to pair up the points of each of the lists, compute the distance of each pair, and sum them up – fairly straightforward:
let distance pair =
((fst pair).X - (snd pair).X) ** 2.0 + ((fst pair).Y - (snd pair).Y) ** 2.0
let evaluate = fun (solution: Point list * Point list) ->
List.zip (fst solution) (snd solution)
|> List.sumBy (fun p -> – distance p)
distance uses the Euclidean distance, and illustrates type inference at work: fst and snd are used to un-pack the first and second elements of a Tuple, so it’s obvious to the compiler the pair is a Tuple, and .X and .Y match the “properties” of our Point record, so it infers that the tuple in question is a Point * Point tuple.
evaluate uses the List.zip function, which “zips” together the 2 lists of points into one list of tuples, pairing points. As a result, we can now apply to each of these pairs the distance function, and return the negative of the sum of the distances (We use the negative because Bumblebee expects the Quality to be increasing for better solutions).
We are almost finished at that point; we just need to provide the Solver with 2 functions – a function to generate new solutions, and a function to mutate an existing solution. The simplest thing that would work to generate new solutions is to shuffle the first of the two lists (no need to shuffle the second one – the result wouldn’t be any “more random”), let’s do that using the Fisher-Yates shuffle:
let shuffle (rng: Random) list =
let rec shuffleUpTo index (array: int[]) =
match index with
| 0 -> array
| _ ->
let swapIndex = rng.Next(index + 1)
let temp = array.[index]
array.[index] <- array.[swapIndex]
array.[swapIndex] <- temp
shuffleUpTo (index - 1) array
let lastIndex = (List.length list - 1)
let shuffled = shuffleUpTo lastIndex [| 0 .. lastIndex |]
List.permute (fun i -> shuffled.[i]) list
let generate = fun (rng: Random) ->
(fst root |> shuffle rng, snd root)
The generate function simply takes in a random number generator; the original tuple of lists of points, root, is captured in a closure, and the function simply returns a new tuple, where the first element is shuffled, and the second one unchanged.
The shuffle function is a direct implementation of the algorithm as described in the link. In previous examples using shuffle, I worked directly on the input list itself, but I realized that this was a performance bottleneck, which negatively impacted speed as the size of the list increased. To avoid that problem, I modified the shuffle a little, so that I now shuffle the indexes of the elements in place, using an array of integers, which has a better lookup time than lists, and apply the shuffled indexes once at the end, permuting the list accordingly.
Almost there – we’ll mutate existing solutions by simply swapping 2 points in the first list, like this:
let swapper (first, second) index =
if index = first then second
elif index = second then first
else index
let swap list (rng: Random) =
let last = List.length list
let first = rng.Next(last)
let second = rng.Next(last)
List.permute (fun i -> swapper (first, second) i) list
let mutate = fun (rng: Random, solution) ->
(swap (fst solution) rng, snd solution)
This can probably be simplified; I re-used some code I wrote while I was very intrigued by the List.permute function…
At that point, we just need to wire up the solver in a fashion similar to the other demo projects, and we are done (complete code at the end of the post). Running this on my machine, I see the algorithm finding a perfect match on 100 points under a minute.
Is one minute good? I am not sure; I suspect the deterministic solution would do better. However, it took me literally 15 minutes to write the entire code – and that brainless code converges very nicely. How about tackling larger problems? The good news is, our algorithm will still find solutions, it will just progress slower. There are two bad news, though: the algorithm has no way to know whether a solution is optimal or not, so in general we won’t know when to stop the search, or whether we are close from the optimum. The other issue is that because of the nature of the search we are performing, the constraint on crossing segments becomes relevant again: our brainless algorithm is looking for the shortest total distance, but the solution it comes up with as implemented are simply improvements found “on the way”, and they could still have crossings.
Still, in spite of all these caveats, I say - not too bad for a whooping 64 lines of code!
Here is the complete implementation of the algorithm as a Console app, using Bumblebee:
open ClearLines.Bumblebee
open System
type Point = { X: float; Y: float }
let Main =
let rng = new Random()
let points = 100
let firstList = [ for i in 0 .. points -> { X = (float)i ; Y = float(i) } ]
let secondList = [ for i in 0 .. points -> { X = (float)i ; Y = float(i) } ]
let root = firstList, secondList
let swapper (first, second) index =
if index = first then second
elif index = second then first
else index
let swap list (rng: Random) =
let last = List.length list
let first = rng.Next(last)
let second = rng.Next(last)
List.permute (fun i -> swapper (first, second) i) list
let shuffle (rng: Random) list =
let rec shuffleUpTo index (array: int[]) =
match index with
| 0 -> array
| _ ->
let swapIndex = rng.Next(index + 1)
let temp = array.[index]
array.[index] <- array.[swapIndex]
array.[swapIndex] <- temp
shuffleUpTo (index - 1) array
let lastIndex = (List.length list - 1)
let shuffled = shuffleUpTo lastIndex [| 0 .. lastIndex |]
List.permute (fun i -> shuffled.[i]) list
let generate = fun (rng: Random) ->
(fst root |> shuffle rng, snd root)
let mutate = fun (rng: Random, solution) ->
(swap (fst solution) rng, snd solution)
let distance pair =
((fst pair).X - (snd pair).X) ** 2.0 + ((fst pair).Y - (snd pair).Y) ** 2.0
let evaluate = fun (solution: Point list * Point list) ->
List.zip (fst solution) (snd solution)
|> List.sumBy (fun p -> - distance p)
let problem = new Problem<Point list * Point list>(generate, mutate, evaluate)
let solver = new Solver<Point list * Point list>()
let foundSomething = fun (msg: SolutionMessage<Point list * Point list>) ->
Console.WriteLine("New solution of quality {0} found at {1}", msg.Quality, msg.DateTime.TimeOfDay)
solver.FoundSolution.Add foundSomething
solver.Search(problem) |> ignore
Console.ReadLine() |> ignore