Nearest Neighbor Classification, Part 2
01 Aug 2012Machine Learning in Action, in F#
Porting Machine Learning in Action from Python to F#
- KNN classification (1)
- KNN classification (2)
- Decision Tree classification
- Naive Bayes classification
- Logistic Regression classification
- SVM classification (1)
- SVM classification (2)
- AdaBoost classification
- K-Means clustering
- SVD
- Recommendation engine
- Code on GitHub
This is the continuation of this post, where I began exploring k-nearest-neighbor classification, a Machine Learning algorithm used to classify items in different categories, based on an existing sample of items that have been properly classified.
Disclaimer: I am new to Machine Learning, and claim no expertise on the topic. I am currently reading Machine Learning in Action, and thought it would be a good learning exercise to convert the book’s samples from Python to F#.
To determine what category an item belongs to, the algorithm measures its distance from each element of the known dataset, and takes a “majority vote” to determine its category, based on its k nearest neighbors.
In our last installment, we wrote a simple classification function, which was doing just that. Today, we’ll continue along Chapter 2, applying our algorithm to real data, and dealing with data normalization.
The dataset: Elections 2008
Rather than use the data sample from the book, I figured it would be more fun to create my own data set. The problem we…ll look into is whether we can predict whether a state voted Republican or Democrat in the 2008 presidential election. Our dataset will consist of the following: the Latitude and Longitude of the State, and its Population. A State is classified as Democrat if the number of votes (i.e. popular vote) recorded for Obama was greater than McCain.
Notes
-
My initial goal was to do this for Cities, but I couldn’t find voting data at that level - so I had to settle for States. The resulting sample is smaller than I would have liked, and also less useful (we can’t realistically use our classifier to produce a prediction for a new State, because the likelihood of a new State joining the Union is fairly small) but it still works well for illustration purposes.
-
Computing distance based on raw Latitude and Longitude wouldn’t be such a great idea in general, because they denote a position on a sphere (very close points may have very different Longitudes); however, given the actual layout of the United States, this will be good enough here.
I gathered the data (see sources at the end) and saved it in a comma-delimited text file “Election2008.txt” (the raw text version is available at the bottom of the post).
First, we need to open that file and parse it into the structure we used in our previous post, with a matrix of observations for each state, and a vector of categories (DEM or REP). That…s easy enough with F#:
let elections =
let file = @"C:\Users\Mathias\Desktop\Elections2008.txt"
let fileAsLines =
File.ReadAllLines(file)
|> Array.map (fun line -> line.Split(','))
let dataset =
fileAsLines
|> Array.map (fun line ->
[| Convert.ToDouble(line.[1]);
Convert.ToDouble(line.[2]);
Convert.ToDouble(line.[3]) |])
let labels = fileAsLines |> Array.map (fun line -> line.[4])
dataset, labels
We open System and System.IO, and use File.ReadAllLines, which returns an array of strings for each line in the text file, and apply string.Split to each line, using the comma as a split-delimiter, which gives us an array of string for each text line. For each row, we then retrieve the dataset part, elements 1, 2 and 3 (the Latitude, Longitude and Population), creating an Array of doubles by converting the strings to doubles. Finally, we retrieve the fourth element of each row, the vote, into an array of labels, and return dataset and labels as a tuple.
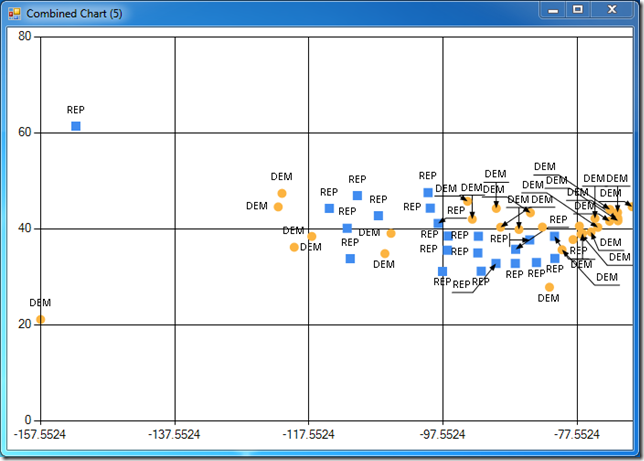
Let’s visualize the result, using the FSharpChart display function we wrote last time. display dataset 1 0 plots Longitude on the X axis, and Latitude on the Y axis, producing a somewhat unusual map of the United States, where we can see the red states / blue states pattern (colored differently), with center states leaning Republican, and Coastal states Democrat:
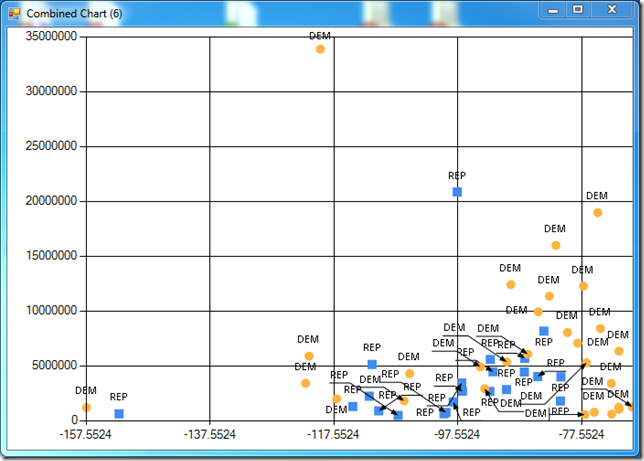
Plotting Latitude against Population produces the following chart, which also displays some clusters:
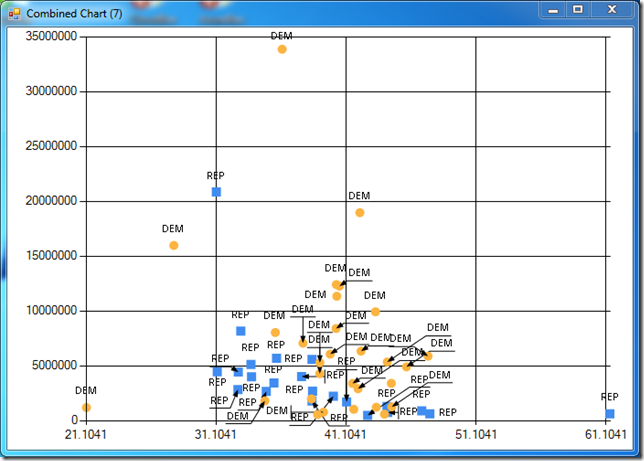
Finally, Longitude versus Population also exhibits some patterns:
Normalizing the data
We could run the algorithm we wrote in the previous post on the data, and measure the distances between observations based on the raw measures, but this would likely produce poor results, because of the discrepancy in scales. Our Latitudes range from about 20 (Hawaii) to 60 (Alaska), while Populations vary from half a million (Washington DC) to over 30 millions (California). Because we compute the distance between observations using the Euclidean distance, differences in Population will have a huge weight in the overall distance, and in effect we would be “ignoring” Latitude and Longitude in our classification.
Consider this: the raw distance between 2 states is given by
Distance (S1, S2) = sqrt ((Pop(S1) - Pop(S2))^2 + (Lat(S1) - Lat(S2))^2 + (Lon(S1) - Lon(S2))^2)
Even if we considered 2 states located as far as possible from each other, at the 2 corners of our map, the distance would look like:
Distance (S1, S2) = sqrt ((Pop(S1) - Pop(S2))^2 + 40^2 + 90^2)
It’s clear that even minimal differences in population in this formula (say, 100,000 inhabitants) will completely dwarf the largest possible effect of geographic distance. If we want to observe the effect of all three dimensions, we need to convert the measurements to a comparable scale, so that differences in Population are comparable, relatively, to differences in Location. To that effect, we will Normalize our dataset. We’ll follow the example of Machine Learning in Action, and normalize each measurement so that its minimal value is 0, and its maximum is 1. Other approaches would be feasible, but this one has the benefit of being fairly straightforward. If we consider Population for instance, what we need to do is:
- Retrieve all the Populations in our Dataset
- Retrieve the minimum and the maximum
- Transform the Population to (Population - minimum) / (maximum - minimum)
Here is what I came up with:
let column (dataset: float [][]) i =
dataset |> Array.map (fun row -> row.[i])
let columns (dataset: float [][]) =
let cols = dataset.[0] |> Array.length
[| for i in 0 .. (cols - 1) -> column dataset i |]
let minMax dataset =
dataset
|> columns
|> Array.map (fun col -> Array.min(col), Array.max(col))
let minMaxNormalizer dataset =
let bounds = minMax dataset
fun (vector: float[]) ->
Array.mapi (fun i v ->
(vector.[i] - fst v) / (snd v - fst v)) bounds
Compared to the Python example, I have to pay a bit of a code tax here, because I chose to use plain F# arrays to model my dataset, instead of using matrices. The column function extracts column i from a dataset, by mapping each row (an observation) to its ith component. columns expands on it, and essentially transposes the matrix, converting it from an array of row vectors to an array of column vectors.
Once we paid that code tax, though, things are pretty easy. minMax retrieves all the columns of a dataset and maps each column to a tuple, containing the minimum and maximum value of each column vector.
It’s probably worth commenting a bit on minMaxNormalizer. If you hover over it in Visual Studio, you’ll see that its signature is
val minMaxNormalizer : float [] [] -> (float [] -> float [])
In other words, minMaxNormalizer is a function which, given a dataset, will return another function, which transforms a vector (or rather a float []) into a vector, normalized between 0 and 1 on each column. The way the function works is simple: first, retrieve the bounds (the minimum and maximum for each column of the dataset), and then declare a function which takes in a float[] and maps each of its components to (Value - column minimum) / (column maximum - column minimum).
This allows us to do things like this:
> let dataset, labels = elections
let normalizer = minMaxNormalizer dataset
let normalized = dataset |> Array.map normalizer;;
We can map our entire dataset using the normalizer, and get a cleaned-up, normalized dataset, which looks like this:
> display normalized labels 1 2;;
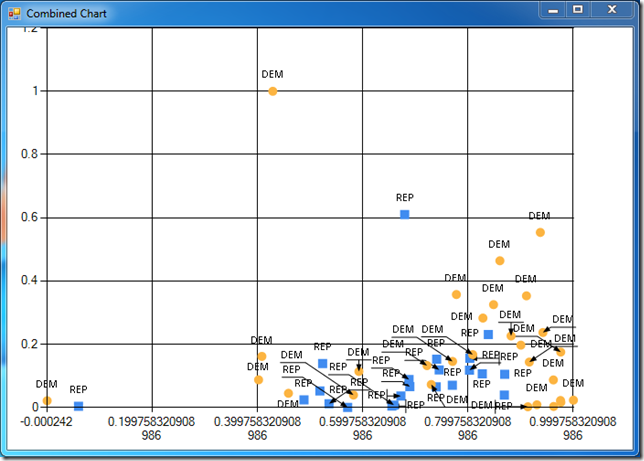
Incidentally, it also illustrates why we may want to consider other Normalization strategies besides min/max. We have a few severe outliers in our sample (California, Hawaii), which stretch the bounds further than reasonable; creating more “robust” normalizers, maybe using mean/variance or fractiles, could be a good idea - but that discussion will be left for another day.
In any case, we are ready to reap the fruits of our labor:
let normalize data (normalizer: float[] -> float[]) =
data |> Array.map normalizer
let classifier dataset labels k =
let normalizer = minMaxNormalizer dataset
let normalized = normalize dataset normalizer
fun subject -> classify (normalizer(subject)) normalized labels k
We declare a normalize function, which takes a dataset and a “generic” normalizer, declared as a function which converts a vector to a vector, and create a classifier, a function which given a dataset with labels and k, the number of nearest neighbors, will compute a normalizer based on the dataset, and create a function which, given a subject (a vector we want to classify), will normalize it and return its classification, using the classify function we wrote in our previous installment.
Note: the normalize function is not necessary here, we could have done without. However, given the previous discussion on using different Normalization strategies, I thought I would leave it in: it would be fairly straightforward to modify the classifier function to accept a
normalizerfunction with the appropriate signature as an input, which would allow us to create various normalization functions and simply pass them in to define how we like to transform our vectors.
So how can we use that? Quite simply, at that point:
> let dataset, labels = elections
let c3 = classifier dataset labels 3;;
c3 is a fully-formed nearest-neighbor classifier, which will use the 3 nearest neighbors. We can use it to determine what a hypothetical large state of 20 million Population, located in the north-east, would have voted:
> c3 [| 48.0; -67.0; 20000000.0 |];;
val it : string * seq<string * float> =
("DEM",
seq [("DEM", 0.173647196); ("DEM", 0.3178208977); ("DEM", 0.3674337337)])
Evaluating the Classifier quality
It’s nice to know that in an alternate universe where New Brunswick, Canada, was actually part of the United States, and had a population of 20,000,000 instead of 750,000, they may have voted Democrat in the 2008 election. However plausible that result, though, it would be nice to quantify how good or bad our classifier is with some hard evidence.
One way to evaluate the quality of our classifier is to use the dataset itself. Take a subset of the dataset as “test subjects”, use the rest to create a classifier, and compare the result of the classification with the known result. If our classifier is working well, we would expect a high proportion of the test subjects to be properly classified.
Nothing subtle here, let’s just print out the classification results on the test subjects, and count the correct ones:
let evaluate dataset (labels: string []) k prop =
let size = dataset |> Array.length
let sample = floor ((float)size * prop) |> (int)
let testSubjects, testLabels = dataset.[0 .. sample-1], labels.[0..sample-1]
let trainData = dataset.[sample .. size-1], labels.[sample .. size-1]
let c = classifier (fst trainData) (snd trainData) k
let results =
testSubjects
|> Array.mapi (fun i e -> fst (c e), testLabels.[i])
results
|> Array.iter (fun e -> printfn "%s %s" (fst e) (snd e))
let correct =
results
|> Array.filter (fun e -> fst e = snd e)
|> Array.length
printfn "%i out of %i called correctly" correct sample
Running this on our sample produces the following:
> evaluate dataset labels 3 0.2;;
REP REP
DEM REP
DEM REP
REP REP
DEM DEM
REP DEM
DEM DEM
DEM DEM
DEM DEM
REP DEM
6 out of 10 called correctly
Not a disaster, but not very impressive, either. We keep 20% of the States for testing purposes, and we get 6 out of 10 right. Let’s crank up k from 3 to 5:
> evaluate dataset labels 5 0.2;;
REP REP
REP REP
REP REP
REP REP
DEM DEM
REP DEM
DEM DEM
DEM DEM
DEM DEM
DEM DEM
9 out of 10 called correctly
Much, much better - and good enough to call it a day, I say.
Conclusion
This covers my excursion of Chapter 2 of Machine Learning in Action and the k-nearest neighbor classification. The book has a nice example using that approach on character recognition, but I think I’ll leave it to my enterprising readers to convert it to F#.
A few comments on my experience with the Python to F# conversion:
-
I debated for a while whether or not to use a Linear Algebra library for this example. I toyed a bit with Math.Net for that purpose, but in the end I decided against it. For that particular example, I found that it didn’t help much, and added some noise to the code: representing the dataset as an array of observation vectors is fairly natural, and the only limitations I could see were that I had to write a function to extract columns, which is straightforward, and that the code is potentially unsafe, in that it doesn’t enforce anywhere that every row should have the same number of elements. There will be plenty of opportunities to do some “real” Linear Algebra later (Support Vector Machines are in Chapter 4…).
-
I thought expressing Normalizers as functions mapping a vector to a vector worked very well. The initial code generating functions is probably less immediately understandable than the Python code, but once the function is created, the code using it is, in my opinion, cleaner and more modular.
-
The evaluation function at the end is still fairly ugly; this is honestly in large part due to my laziness. Somewhat relatedly, the attentive reader may have noticed that I jumped from k = 3 to k = 5 in the tests I performed. This is not an accident - I realized that there is a potential bug in the approach. The classifier picks the largest group among the nearest neighbors, but in case of an even number, it’s possible to have a tie, and the classifier will simply pick the first group (which seems somewhat incorrect), a problem avoided altogether with odd numbers. I began cleaning up the return type of the classifier (the current type, Key * Key seq, is fairly ugly), which would also allow for a cleaner evaluation function, maybe using a discriminated union like
Decision = Inconclusive | Classification of string. I’ll leave that as a footnote for now, and maybe revisit later. -
While at times not-too-user-friendly, FSharpChart is pretty awesome - being able to generate charts while working in Visual Studio / fsi and exploring data, in the same language, is great.
That’s it for today! Again, I claim no expertise in Machine Learning, so your comments and suggestions are highly welcome. I’ll try to put this code up in GitHub, once I figure out a good way to organize the solution. Next in line: Naïve Bayes classification, which should be pretty fun.
Code
// Replace this path with the location where NuGet (or you) installed MSDN.FSharpChart:
#r @"C:\Users\Mathias\Documents\Visual Studio 2010\Projects\MachineLearningInAction\packages\MSDN.FSharpChart.dll.0.60\lib\MSDN.FSharpChart.dll"
#r @"System.Windows.Forms.DataVisualization.dll"
open System
open System.IO
open System.Drawing
open MSDN.FSharp.Charting
let createDataset =
[| [| 1.0; 0.9 |]
[| 0.8; 1.0 |]
[| 0.8; 0.9 |]
[| 0.0; 0.1 |]
[| 0.3; 0.0 |]
[| 0.1; 0.1 |] |],
[| "A"; "A"; "A"; "B"; "B"; "B" |]
let display (dataset: float[][]) (labels: string []) i j =
let byLabel =
dataset
|> Array.map (fun e -> e.[i], e.[j])
|> Array.zip labels
let uniqueLabels = Seq.distinct labels
FSharpChart.Combine
[ for label in uniqueLabels ->
let data =
Array.filter (fun e -> label = fst e) byLabel
|> Array.map snd
FSharpChart.Point(data) :> ChartTypes.GenericChart
|> FSharpChart.WithSeries.Marker(Size=10)
|> FSharpChart.WithSeries.DataPoint(Label=label)
]
|> FSharpChart.Create
let distance v1 v2 =
Array.zip v1 v2
|> Array.fold (fun sum e -> sum + pown (fst e - snd e) 2) 0.0
|> sqrt
let classify subject dataset labels k =
dataset
|> Array.map (fun row -> distance row subject)
|> Array.zip labels
|> Array.sortBy snd
|> Array.toSeq
|> Seq.take k
|> Seq.groupBy fst
|> Seq.maxBy (fun g -> Seq.length (snd g))
let column (dataset: float [][]) i =
dataset |> Array.map (fun row -> row.[i])
let columns (dataset: float [][]) =
let cols = dataset.[0] |> Array.length
[| for i in 0 .. (cols - 1) -> column dataset i |]
let minMax dataset =
dataset
|> columns
|> Array.map (fun col -> Array.min(col), Array.max(col))
let minMaxNormalizer dataset =
let bounds = minMax dataset
fun (vector: float[]) ->
Array.mapi (fun i v ->
(vector.[i] - fst v) / (snd v - fst v)) bounds
let normalize data (normalizer: float[] -> float[]) =
data |> Array.map normalizer
let classifier dataset labels k =
let normalizer = minMaxNormalizer dataset
let normalized = normalize dataset normalizer
fun subject -> classify (normalizer(subject)) normalized labels k
let elections =
let file = @"C:\Users\Mathias\Desktop\Elections2008.txt"
let fileAsLines =
File.ReadAllLines(file)
|> Array.map (fun line -> line.Split(','))
let dataset =
fileAsLines
|> Array.map (fun line ->
[| Convert.ToDouble(line.[1]);
Convert.ToDouble(line.[2]);
Convert.ToDouble(line.[3]) |])
let labels = fileAsLines |> Array.map (fun line -> line.[4])
dataset, labels
let evaluate dataset (labels: string []) k prop =
let size = dataset |> Array.length
let sample = floor ((float)size * prop) |> (int)
let testSubjects, testLabels = dataset.[0 .. sample-1], labels.[0..sample-1]
let trainData = dataset.[sample .. size-1], labels.[sample .. size-1]
let c = classifier (fst trainData) (snd trainData) k
let results =
testSubjects
|> Array.mapi (fun i e -> fst (c e), testLabels.[i])
results
|> Array.iter (fun e -> printfn "%s %s" (fst e) (snd e))
let correct =
results
|> Array.filter (fun e -> fst e = snd e)
|> Array.length
printfn "%i out of %i called correctly" correct sample
Raw dataset (State, Latitude, Longitude, 2000 Population, Vote)
AL,32.7990,-86.8073,4447100,REP
AK,61.3850,-152.2683,626932,REP
AZ,33.7712,-111.3877,5130632,REP
AR,34.9513,-92.3809,2673400,REP
CA,36.1700,-119.7462,33871648,DEM
CO,39.0646,-105.3272,4301261,DEM
CT,41.5834,-72.7622,3405565,DEM
DE,39.3498,-75.5148,783600,DEM
DC,38.8964,-77.0262,572059,DEM
FL,27.8333,-81.7170,15982378,DEM
GA,32.9866,-83.6487,8186453,REP
HI,21.1098,-157.5311,1211537,DEM
ID,44.2394,-114.5103,1293953,REP
IL,40.3363,-89.0022,12419293,DEM
IN,39.8647,-86.2604,6080485,DEM
IA,42.0046,-93.2140,2926324,DEM
KS,38.5111,-96.8005,2688418,REP
KY,37.6690,-84.6514,4041769,REP
LA,31.1801,-91.8749,4468976,REP
ME,44.6074,-69.3977,1274923,DEM
MD,39.0724,-76.7902,5296486,DEM
MA,42.2373,-71.5314,6349097,DEM
MI,43.3504,-84.5603,9938444,DEM
MN,45.7326,-93.9196,4919479,DEM
MS,32.7673,-89.6812,2844658,REP
MO,38.4623,-92.3020,5595211,REP
MT,46.9048,-110.3261,902195,REP
NE,41.1289,-98.2883,1711263,REP
NV,38.4199,-117.1219,1998257,DEM
NH,43.4108,-71.5653,1235786,DEM
NJ,40.3140,-74.5089,8414350,DEM
NM,34.8375,-106.2371,1819046,DEM
NY,42.1497,-74.9384,18976457,DEM
NC,35.6411,-79.8431,8049313,DEM
ND,47.5362,-99.7930,642200,REP
OH,40.3736,-82.7755,11353140,DEM
OK,35.5376,-96.9247,3450654,REP
OR,44.5672,-122.1269,3421399,DEM
PA,40.5773,-77.2640,12281054,DEM
RI,41.6772,-71.5101,1048319,DEM
SC,33.8191,-80.9066,4012012,REP
SD,44.2853,-99.4632,754844,REP
TN,35.7449,-86.7489,5689283,REP
TX,31.1060,-97.6475,20851820,REP
UT,40.1135,-111.8535,2233169,REP
VT,44.0407,-72.7093,608827,DEM
VA,37.7680,-78.2057,7078515,DEM
WA,47.3917,-121.5708,5894121,DEM
WV,38.4680,-80.9696,1808344,REP
WI,44.2563,-89.6385,5363675,DEM
WY,42.7475,-107.2085,493782,REP
Sources
Election 2008 results: Dave Leip’s Atlas of US Presidential Elections.
Latitudes & Longitudes: MaxMind Average Latitude and Longitude for US States.
Population: Wikipedia List of U.S. states and territories by population.
