Fun with L-Systems

I had the great pleasure to speak at CodeMash this week, and, on my way back, ended up spending a couple of hours at the Atlanta airport waiting for my connecting flight back to the warmer climate of San Francisco – a perfect opportunity for some light-hearted coding fun. A couple of days earlier, I came across this really nice tweet, rendering the results of an L-system:

{start:'FFPF',rules:{F:'PF++F[FF-F+PF+FPP][F]FFPF',P:''},'α':60} pic.twitter.com/JZGDV4ghFy

— LSystemBot 2.0 (@LSystemBot) January 10, 2015

I ended up looking up L-systems on Wikipedia, and thought this would make for some fun coding exercise. In a nutshell, a L-system is a grammar. It starts with an alphabet of symbols, and a set of rules which govern how each symbol can be transformed into another chain of symbols. By applying these rules to a starting state (the initial axiom), one can evolve it into a succession of states, which can be seen as the growth of an organism. And by mapping each symbol to operations in a logo/turtle like language, each generation can then be rendered as a graphic.

So how could we go about coding this in F#? If you are impatient, you can find the final result as a gist here.

First, I started with representing the core elements of an L-System with a couple of types:

type Symbol = | Sym of char

type State = Symbol list

type Rules = Map<Symbol,State>

type LSystem =
  { Axiom:State
    Rules:Rules }

A symbol is a char, wrapped in a single-case discriminated union, and a State is simply a list of Symbols. We define the Rules that govern the transformation of Symbols by a Map, which associates a particular Symbol with a State, and an L-System is then an Axiom (the initial State), with a collection of Rules.

Let’s illustrate this on the second example from the Wikipedia page, the Pythagoras tree. Our grammar contains 4 symbols, 0, 1, [ and ], we start with a 0, and we have 2 rules, (1 → 11), and (0 → 1[0]0). This can be encoded in a straightforward manner in our domain, like this:

let lSystem =
  { Axiom = [ Sym('0') ]
    Rules = [ Sym('1'), [ Sym('1'); Sym('1') ]
              Sym('0'), [ Sym('1'); Sym('['); Sym('0'); Sym(']'); Sym('0') ]]
            |> Map.ofList }

Growing the organism by applying the rules is fairly straightforward: given a State, we traverse the list of Symbols, look up for each of them if there is a matching rule, and perform a substitution if it is found, leaving it unchanged otherwise:

(*
Growing from the original axiom
by applying the rules
*)

let applyRules (rs:Rules) (s:Symbol) =
  match (rs.TryFind s) with
  | None -> [s]
  | Some(x) -> x

let evolve (rs:Rules) (s:State) =
  [ for sym in s do yield! (applyRules rs sym) ]

let forward (g:LSystem) =
  let init = g.Axiom
  let gen = evolve g.Rules
  init |> Seq.unfold (fun state -> Some(state, gen state))

// compute nth generation of lSystem
let generation gen lSystem =
  lSystem
  |> forward
  |> Seq.nth gen
  |> Seq.toList

What does this give us on the Pythagoras Tree?

> lSystem |> generation 1;;
val it : Symbol list = [Sym '1'; Sym '['; Sym '0'; Sym ']'; Sym '0']

Nice and crisp – that part is done. Next up, rendering. The idea here is that for each Symbol in a State, we will perform a substitution with a sequence of instructions, either a Move, drawing a line of a certain length, or a Turn of a certain Angle. We will also have a Stack, where we can Push or Pop the current position of the Turtle, so that we can for instance store the current position and direction on the stack, perform a couple of moves with a Push, and then return to the previous position by a Pop, which will reset the turtle to the previous position. Again, that lends itself to a very natural model:

(*
Modelling the Turtle/Logo instructions
*)

type Length = | Len of float
type Angle = | Deg of float

// override operator later
let add (a1:Angle) (a2:Angle) =
  let d1 = match a1 with Deg(x) -> x
  let d2 = match a2 with Deg(x) -> x
  Deg(d1+d2)

type Inst =
  | Move of Length
  | Turn of Angle
  | Push
  | Pop

let Fwd x = Move(Len(x))
let Lft x = Turn(Deg(x))
let Rgt x = Turn(Deg(-x))

We can now transform our L-system state into a list of instructions, and convert them into a sequence of Operations, in that case Drawing lines between 2 points:

type Pos = { X:float; Y:float; }
type Dir = { L:Length; A:Angle }

type Turtle = { Pos:Pos; Dir:Dir }
type ProgState = { Curr:Turtle; Stack:Turtle list }

let turn angle turtle =
  let a = turtle.Dir.A |> add angle
  { turtle with Dir = { turtle.Dir with A = a } }

type Translation = Map<Symbol,Inst list>

type Ops = | Draw of Pos * Pos

let pi = System.Math.PI

let line (pos:Pos) (len:Length) (ang:Angle) =
  let l = match len with | Len(l) -> l
  let a = match ang with | Deg(a) -> (a * pi / 180.)
  { X = pos.X + l * cos a ; Y = pos.Y + l * sin a }

let execute (inst:Inst) (state:ProgState) =
  match inst with
  | Push -> None, { state with Stack = state.Curr :: state.Stack }
  | Pop ->
    let head::tail = state.Stack // assumes more Push than Pop
    None, { state with Curr = head; Stack = tail }
  | Turn(angle) ->
    None, { state with Curr =  state.Curr |> turn angle }
  | Move(len) ->
    let startPoint = state.Curr.Pos
    let endPoint = line startPoint len state.Curr.Dir.A
    Some(Draw(startPoint,endPoint)), { state with Curr = { state.Curr with Pos = endPoint } }

let toTurtle (T:Translation) (xs:Symbol list) =

  let startPos = { X = 400.; Y = 400. }
  let startDir = { L = Len(0.); A = Deg(0.) }
  let init =
    { Curr = { Pos = startPos; Dir = startDir }
      Stack = [] }
  xs
  |> List.map (fun sym -> T.[sym])
  |> List.concat
  |> Seq.scan (fun (op,state) inst -> execute inst state) (None,init)
  |> Seq.map fst
  |> Seq.choose id

We simply map each Symbol to a List of instructions, transform the list of symbols into a list of instructions, and maintain at each step the current position and direction, as well as a Stack (represented as a list) of positions and directions. How does it play out on our Pythagoras Tree? First, we define the mapping from Symbols to Instructions:

let l = 1.
let T =
  [ Sym('0'), [ Fwd l; ]
    Sym('1'), [ Fwd l; ]
    Sym('['), [ Push; Lft 45.; ]
    Sym(']'), [ Pop; Rgt 45.; ] ]
  |> Map.ofList

… and we simply send that toTurtle, which produces a list of Draw instructions:

> lSystem |> generation 1 |> toTurtle T;;
val it : seq<Ops> =
  seq
  [ Draw ({X = 400.0; Y = 400.0;},{X = 401.0; Y = 400.0;});
    Draw ({X = 401.0; Y = 400.0;},{X = 401.7071068; Y = 400.7071068;});
    Draw ({X = 401.0; Y = 400.0;},{X = 401.7071068; Y = 399.2928932;})]

Last step – some pretty pictures. We’ll simply generate a html document, rendering the image using SVG, by creating one SVG line per Draw instruction:

let header = """
<!DOCTYPE html>
<html>
<body>
<svg height="800" width="800">"""

let footer = """
</svg>
</body>
</html>
"""

let toSvg (ops:Ops seq) =
  let asString (op:Ops) =
    match op with
    | Draw(p1,p2) ->
      sprintf """<line x1="%f" y1="%f" x2="%f" y2="%f" style="stroke:rgb(0,0,0);stroke-width:1" />""" p1.X p1.Y p2.X p2.Y

  [ yield header
    for op in ops -> asString op
    yield footer ]
  |> String.concat "\n"

open System.IO

let path = "C:/users/mathias/desktop/lsystem.html"
let save template = File.WriteAllText(path,template)

And we are pretty much done:

> lSystem |> generation 8 |> toTurtle T |> toSvg |> save;;
val it : unit = ()

… which produces the following graphic:

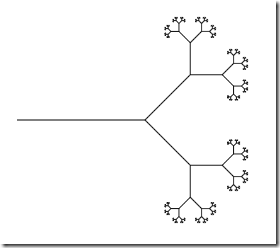
Pretty neat! Just for fun, I replicated the Sierpinski Triangle example as well:

let sierpinski () =

  let lSystem =
    { Axiom = [ Sym('A') ]
      Rules =
        [ Sym('A'), [ Sym('B'); Sym('>'); Sym('A'); Sym('>'); Sym('B') ]
          Sym('B'), [ Sym('A'); Sym('<'); Sym('B'); Sym('<'); Sym('A') ]]
        |> Map.ofList }

  let l = 1.
  let T =
    [ Sym('A'), [ Fwd l; ]
      Sym('B'), [ Fwd l; ]
      Sym('>'), [ Lft 60.; ]
      Sym('<'), [ Rgt 60.; ] ]
    |> Map.ofList

  lSystem
  |> generation 9
  |> toTurtle T
  |> toSvg
  |> save

… which results in the following picture:

That’s it for tonight! I had a lot of fun coding this (it certainly made the flight less boring), and found the idea of converting code to turtle instructions, with a stack, pretty interesting. Hope you enjoyed it, and if you end up playing with this, share your creations on Twitter and ping me!

Gist for the whole code here