Basic Regression Tree
14 Aug 2016In our previous installment, we began exploring Gradient Boosting, and outlined how by combining extremely crude regression models - stumps - we could iteratively create a decent prediction model for the quality of wine bottles, using one Feature, one of the chemical measurements we have available.
In and of itself, this is an interesting result: the approach allows us to aggregate mediocre indicators together into a predictor that is better than its individual parts. However, so far, we are using only a tiny subset of the information available. Why restrict ourselves to a single Feature, and not use all of them? And, if the approach works with something as weak as a stump, perhaps we can do better, by aggregating less trivial prediction models?
This will be our goal today: we will create a Regression Tree, which we will in a future installment use in place of stumps in our Boosting procedure.
Regression Trees
Full code for this post available here as a Gist
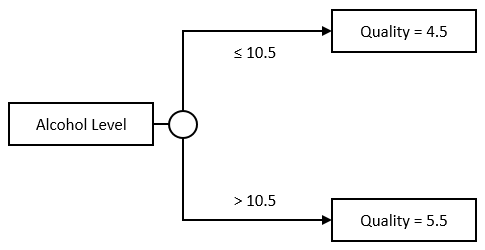
The Stump model is rather simple: we take a Feature and a split value, the threshold. If the input value is under that threshold, we predict the average output value computed across examples under the threshold, otherwise, we do the opposite:
Or, in code:
type Wine = CsvProvider<"data/winequality-red.csv",";",InferRows=1500>
type Observation = Wine.Row
type Feature = Observation -> float
type Example = Observation * float
type Predictor = Observation -> float
let learnStump (sample:Example seq) (feature:Feature) threshold =
let under =
sample
|> Seq.filter (fun (obs,lbl) -> feature obs <= threshold)
|> Seq.averageBy (fun (obs,lbl) -> lbl)
let over =
sample
|> Seq.filter (fun (obs,lbl) -> feature obs > threshold)
|> Seq.averageBy (fun (obs,lbl) -> lbl)
fun obs ->
if (feature obs <= threshold)
then under
else over
A regression tree extends the idea further. Instead of limiting ourselves to a single threshold, we can further divide each group, and create trees like this one for instance:
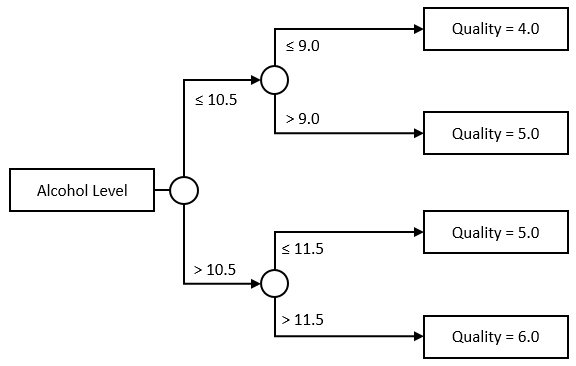
Nothing forces us to keep the tree symmetrical, or to use a single Feature, though. This would be a perfectly acceptable tree as well:
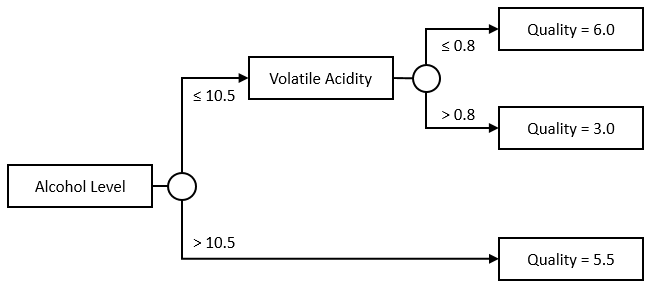
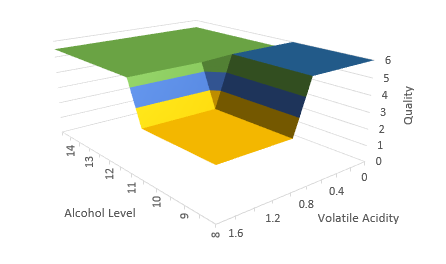
The nice thing about trees is, they are pretty flexible, and very easy to interpret. With a tree, we can incorporate multiple features and their interactions. In our example, we are really modelling Quality as a surface, instead of a simple line in the stump example:
The resulting model can be expressed in a very understandable form:
If the Alcohol Level is over 10.5, the Quality is 5.5; Otherwise, check the Volatile Acidity. If it is below 0.8, the Quality is 6.0, otherwise it is 3.0.
Creating a Tree
How can we go about representing and learning a Tree?
As it turns out, the representation is fairly straightforward. A Tree can be seen as a recursive data structure: either we reached a terminal Leaf, which gives us a prediction, or we reach a Branch, where, based on a Feature and associated split value, we will find 2 new Trees, one for values under the split value, another for values above the split.
That is a match in heaven for a Discriminated Union:
type Tree =
| Leaf of float
| Branch of (Feature * float) * Tree * Tree
Creating manually the “complex” tree we described above can be done along these lines:
let exampleTree =
// we start with a branch
Branch(
// we split on Alcohol level, 10.5
(``Alcohol Level``, 10.5),
// if alcohol level is under 10.5,
// we have another branch
Branch(
// we split on Volatile Acidity, 0.8
(``Volatile Acidity``, 0.8),
// if acidity is under 0.8,
// we predict 6.0
Leaf(6.0),
// otherwise we predict 3.0
Leaf(3.0)
),
// if alcohol is over 10.5,
// we predict 5.5
Leaf(5.5)
)
How do we go about making predictions with a Tree? We simply walk it down recursively:
let rec predict (tree:Tree) (obs:Observation) =
match tree with
| Leaf(prediction) -> prediction
| Branch((feature,split),under,over) ->
let featureValue = feature obs
if featureValue <= split
then predict under obs
else predict over obs
Let’s try it out on our example:
predict exampleTree (reds.Rows |> Seq.head)
> val it : float = 6.0
Note that, if we use partial application:
let examplePredictor = predict exampleTree
… we get back a function, examplePredictor, which happens to have exactly the signature we defined earlier for a Predictor:
val examplePredictor : (Observation -> float)
As a result, we can immediately re-use the sumOfSquares error function we wrote last time, and evaluate how good our tree is fitting the dataset:
let sumOfSquares (sample:Example seq) predictor =
sample
|> Seq.sumBy (fun (obs,lbl) ->
pown (lbl - predictor obs) 2)
let redSample =
reds.Rows
|> Seq.map (fun row -> row, row.Quality |> float)
sumOfSquares redSample examplePredictor
val it : float = 1617.0
The result is pretty terrible - but then, I picked the tree values randomly. Can we automatically learn a “good” Tree?
Learning a Tree
If you recall, the approach we followed to learn a “good” stump was the following: for a given Feature, try out various possible split values, and pick the one that gives us the smallest error, defined as the sumOfSquares between the predicted and actual values.
We can use the same idea for a Tree. Instead of stopping once we found a good split, we will simply repeat the same process, and look for a good split in each of the two samples we got after the split. Also, instead of searching for a split on a single Feature, we will now consider all of them, and select the best split across all available Features.
That smells like recursion. As a first pass, we will re-use some of the code we wrote last time, the learnStump and evenSplits functions, and whip together a quick-and-dirty tree learning function, disregarding any performance consideration:
let rec learnTree (sample:Example seq) (features:Feature list) (depth:int) =
if depth = 0
then
// we reached maximum depth, and
// predict the sample average.
let avg = sample |> Seq.averageBy snd
Leaf(avg)
else
let (bestFeature,bestSplit) =
// create all feature * split combinations
seq {
for feature in features do
let splits = evenSplits sample feature 10
for split in splits -> feature,split
}
// find the split with the smallest error
|> Seq.minBy (fun (feature,split) ->
let predictor = learnStump sample feature split
sumOfSquares sample predictor)
// split the sample following the split
let under =
sample
|> Seq.filter (fun (obs,_) ->
bestFeature obs <= bestSplit)
let over =
sample
|> Seq.filter (fun (obs,_) ->
bestFeature obs > bestSplit)
// learn the corresponding trees
let underTree = learnTree under features (depth - 1)
let overTree = learnTree over features (depth - 1)
// and create the corresponding branch
Branch((bestFeature,bestSplit),underTree,overTree)
Let’s try this out, with a Tree that should be equivalent to the first stump we created last time:
let originalStump = learnTree redSample [ ``Alcohol Level`` ] 1
sumOfSquares redSample (predict originalStump)
val it : float = 864.4309287
Good news - we get the same result. Now let’s crank it up a notch:
let deeperTree = learnTree redSample [``Alcohol Level``;``Volatile Acidity``] 4
sumOfSquares redSample (predict deeperTree)
val it : float = 680.1290569
This is significantly better that the best result we achieved by ensembling stumps, 811.4601191.
Cleaning up our act (a bit)
We have a decent-looking Tree learning algorithm. However, not everything is perfect. For instance, emboldened by our success, we could try to increase the depth a bit.
let explodingTree = learnTree redSample [``Alcohol Level``] 5
System.ArgumentException: The step of a range cannot be zero.
Parameter name: step
// long list of F# complaints follows
Uh-oh. What is happening here?
As we recurse deeper in the Tree, we split the samples further and further, and have less and less data to train our stump on. One thing which might happen for instance is that we are left only with examples sharing the same label. In that situation, generating even splits is going to cause issues, because the width in [ min + width .. width .. max - width ] (our evenly-spaced splits) will be 0.0.
This indicates a first problem, namely, that there might not be any good split to use for a given sample.
Beyond that, the design is also a bit problematic. The choice of 10 even splits is quite arbitrary; we might want to use 3, or 42 even splits, or use different strategies altogether (splits of same size, every possible distinct value, …). Our evenSplits function is hard-coded deep inside the algorithm - it would be much nicer if we could inject any split function as an argument.
In a similar vein, assuming we are comfortable with using stumps / binary splits, the choice of our error metric is also quite arbitrary. We might want to use something else that the sum of squared prediction errors (Manhattan distance, variance reduction, …). Again, that function is buried deep inside - we would like to use any reasonable cost function we think relevant to the problem.
Finally, we are picking the split that yields the best cost. However, that split is not guaranteed to be an improvement. As an example, every observation in the sample could have the same label, in which case no split will improve our predictions. If the resulting cost is the same as before, it is pointless to split, and we might as well spare the algorithm a useless deeper search.
In short,
- we are not guaranteed to have splits for every sample,
- we should split only when strict cost improvements are found,
- we would like to decide what splits to use,
- we would like to decide what cost metric to use.
We are probably going slightly overboard here; the only real problem we have is the first one. At the same time, why not have a bit of fun!
I am going to start with defining a couple of type aliases and utilities:
let underOver (sample:Example seq) (feat:Feature,split:float) =
let under = sample |> Seq.filter (fun (obs,_) -> feat obs <= split)
let over = sample |> Seq.filter (fun (obs,_) -> feat obs > split)
under,over
type Splitter = Example seq -> Feature -> float list
type Cost = Example seq -> float
underOver simply takes a sample, and partitions it into 2 samples, based on a feature and a split value. Splitter is a function that, given a sample and a Feature, will produce a (potentially empty) list of values we could split on. Cost simply measures how good a sample is.
Given these elements, we can now rewrite our learnTree function along these lines:
let rec learnTree (splitter:Splitter,cost:Cost) (sample:Example seq) (features:Feature list) (depth:int) =
if depth = 0
then
let avg = sample |> Seq.averageBy snd
Leaf(avg)
else
let initialCost = cost sample
let candidates =
// build up all the feature/split candidates,
// and their associated sample splits
seq {
for feature in features do
let splits = splitter sample feature
for split in splits ->
let under,over = underOver sample (feature,split)
(feature,split),(under,over)
}
// compute and append cost of split
|> Seq.map (fun (candidate,(under,over)) ->
candidate,(under,over), cost under + cost over)
// retain only candidates with strict cost improvement
|> Seq.filter (fun (candidate,(under,over),splitCost) ->
splitCost < initialCost)
if (Seq.isEmpty candidates)
then
let avg = sample |> Seq.averageBy snd
Leaf(avg)
else
let ((bestFeature,bestSplit),(under,over),spliCost) =
candidates
|> Seq.minBy (fun (_,_,splitCost) -> splitCost)
let underTree = learnTree (splitter,cost) under features (depth - 1)
let overTree = learnTree (splitter,cost) over features (depth - 1)
Branch((bestFeature,bestSplit),underTree,overTree)
Trying it out
Does it work? Let’s try it out:
let evenSplitter n (sample:Example seq) (feature:Feature) =
let values = sample |> Seq.map (fst >> feature)
let min = values |> Seq.min
let max = values |> Seq.max
if min = max
then []
else
let width = (max-min) / (float (n + 1))
[ min + width .. width .. max - width ]
let sumOfSquaresCost (sample:Example seq) =
let avg = sample |> Seq.averageBy snd
sample |> Seq.sumBy (fun (_,lbl) -> pown (lbl - avg) 2)
let stableTree = learnTree (evenSplitter 10,sumOfSquaresCost) redSample [``Alcohol Level``;``Volatile Acidity``] 10
sumOfSquares redSample (predict stableTree)
This time, nothing explodes - and the value we get is
val it : float = 331.1456491
The nice thing here is that at that point, all it takes to create and try new trees is a specification for the cost and split functions, and a list of features. We can, for instance, create a Tree using every feature we have available:
let features = [
``Alcohol Level``
``Chlorides``
``Citric Acid``
``Density``
``Fixed Acidity``
``Free Sulfur Dioxide``
``PH``
``Residual Sugar``
``Total Sulfur Dioxide``
``Volatile Acidity``
]
let fullTree = learnTree (evenSplitter 5,sumOfSquaresCost) redSample features 10
The results are pretty decent, too:
Out of curiosity, I also performed a crude training vs. testing analysis, to get a feel for potential over-fitting issues.
The result we observe is typical of trees: as we increase depth, the error on the training sample steadily decreases, indicating that deeper tree fit the data better and better. However, the testing sample tells a different story: for a little while, error on the training and testing samples match fairly closely, but after we reach a certain depth (here, 3), they start diverging. While our tree fit the training sample better and better, that improvement doesn’t generalize to other samples, as we can see on the testing sample; at that point, we are over-fitting. In our particular case, this means that we shouldn’t put much trust in trees deeper than 3.
Conclusion
At that point, we have a working regression tree algorithm. It’s not perfect; in particular, we largely ignored any performance consideration. Or, stated more bluntly, performance is terrible ;) Still, the result has a couple nice features, the code is fairly simple, and… it works!
Trees are quite an interesting topic, which we only covered very superficially here. Still, we will leave it at that for now, and focus back on our initial goal, gradient boosting. All we needed was something a bit better than stumps to iteratively fit residuals. We have that now, with regression tree that allow us to learn a predictor using every feature we have available. In our next installments, we will look at replacing stumps with trees, and see where that leads us.
