Picking from Random Tables

07 Jan 2022

Once again, I started a weekend project on a minor problem that ended up being more involved than expected. This time, the topic is random tables. Random tables are used often in role playing games, to create random items or ideas on the fly, based on a dice roll.

The process of rolling physical dice is fun, but can be slow, so I started coding some of these random tables to help me keep the flow going during games. As an example, this page creates “random citizens” you might encounter in the fictional city of Doskvol. Every roll will produce a new citizen, like this one for instance:

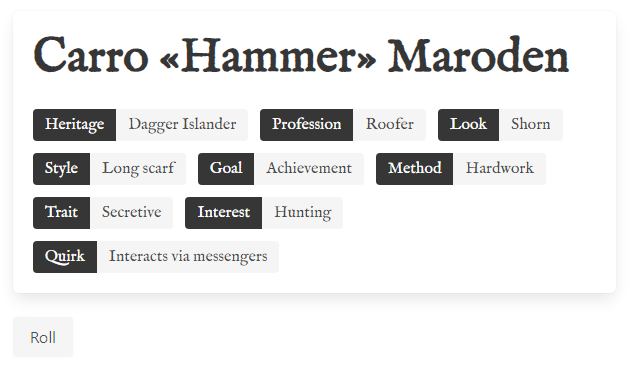
Random Doskvol Citizen

In general, these are not too complicated. However, some generators can become quite tricky. As an example, “The Perilous Wilds” has complex tables like this one:

Ability (roll 1d12)
---
bless/curse
entangle/trap/ensnare
// omitted entries
MAGIC TYPE
drain life/magic
immunity: ELEMENT
read/control minds
roll twice on this table

I have had a lot of fun so far trying to model these tables in F#, so I figured perhaps sharing my exploration would make an interesting topic!

Picking from simple tables

Conceptually, a Table is a finite collection of entries, which we want to randomly pick from. Tables come in two flavors: “flat tables” (every entry has the same chance to be selected), and weighted tables (entries have different weights, describing their relative probability of being picked).

Let’s start with “flat tables”. All we need here is a random generator, and a list of entries:

let uniform (rng: Random) (uniform: List<_>) =
    let i = rng.Next(0, uniform.Length)
    uniform.[i]

Note: from a performance standpoint, an array would be better, but I will stick with lists here. Performance is not really a concern here, and lists have a nicer syntax for a DSL.

let alignment = [
    "chaotic"
    "evil"
    "neutral"
    "good"
    "lawful"
    ]
let rng = Random ()

… which we can use to produces random alignments, like so:

> uniform rng alignment;;
val it: string = "evil"

How about weighted tables? That is a little more work. We need to have a strictly positive weight for each entry, and pick accordingly. After some internal debate, I decided to wrap the Weights into their own type, to enforce that they are indeed positive:

type Weight =
    private | W of int
    with
    static member create w =
        if w <= 0
        then failwith $"Invalid weight {w}: pick weight must be positive."
        else W w
    member this.Value =
        this
        |> function | W w -> w

We can now use weights to pick from a weighted list, like so: we roll a number, and walk down the list until the roll is higher than the running total of the weights.

let weighted (rng: Random) (weighted: list<Weight * _>) =
    let total =
        weighted
        |> List.sumBy (fun (w, _) -> w.Value)
    let roll = rng.Next (0, total) + 1
    let rec search acc (entries: list<Weight * _>) =
        match entries with
        | [] -> failwith "no entry to pick from table"
        | (weight, value) :: tl ->
            let acc = acc + weight.Value
            if acc >= roll
            then value
            else search acc tl
    search 0 weighted

For convenience, we also create a function, weight, to simplify our syntax:

let weight (i: int) = Weight.create i

At that point, we can create weighted lists:

let size = [
    weight 1, "tiny"
    weight 2, "small"
    weight 3, "medium"
    weight 2, "large"
    weight 1, "huge"
    ]

… and pick from them:

> weighted rng size;;
val it: string = "medium"

A quick sanity check confirms that the distribution looks plausible:

List.init 100000 (fun _ -> weighted rng size)
|> List.countBy id

val it: (string * int) list =
  [("large", 22343); ("medium", 33445); ("small", 21999); ("tiny", 11095);
   ("huge", 11118)]

As a final step, let’s wrap the 2 types of tables into one type, Distribution:

type Distribution<'T> =
    | Uniform of list<'T>
    | Weighted of list<Weight * 'T>
    with
    member this.Length =
        match this with
        | Uniform xs -> xs.Length
        | Weighted xs -> xs.Length

This allows us now to write a convenience function, pick, which will pick at random based on the type of table / distribution:

let from (rng: Random) (distribution: Distribution<_>) =
    match distribution with
    | Uniform distribution -> uniform rng distribution
    | Weighted distribution -> weighted rng distribution

Picking from more complex tables

We can now pick from simple tables. However, the sample table we started with is a bit more complex than what we can currently handle:

Ability
---
1  bless/curse
2  entangle/trap/ensnare
// omitted entries

How can we approach this? I would read this table as follows: “On a 1, the result is bless or curse”. That is, with equal probability, I should get bless or curse. So what I would like to write is something along these lines:

let ability = [
    Or [ "bless"; "curse" ]
    Or [ "entangle"; "trap"; "ensnare" ]
    ]

The problem, though, is that if we do that, we can’t add a simple string entry to the list anymore. Let’s create a new type, then, wrapping simple entries as a case of a Discriminated Union. For good measure, we will also add the And case, which seems like an obvious extension:

type Entry<'T> =
    | Item of 'T
    | And of list<Entry<'T>>
    | Or of list<Entry<'T>>

We can now write “hybrid” tables, like so:

let ability = [
    Item "some ability"
    Or [ "bless"; "curse" ]
    ]

Due to the recursive nature of our representation, we can also write potentially even more intricate expressions, like this one:

let complexTable = [
    Item "human"
    And [ Or [ Item "human"; Item "goblin" ]; Item "undead" ]
    ]

… where the second entry describes a creature that could be either an undead human, or an undead goblin.

So how do we pick from that type of list now? All we need is an evaluation function like this:

let rec eval (rng: Random) (entry: Entry<'T>) =
    match entry with
    | Item item -> List.singleton item
    | And entries -> entries |> List.collect (eval rng)
    | Or entries -> entries |> Pick.uniform rng |> eval rng

> complexTable |> uniform rng |> eval rng
val it: string list = ["goblin"; "undead"]

Note: I debated creating a type to represent non-empty lists, because the picker will fail for an empty Or case, but that was a bit more work than what I felt like. A simpler fix is to match on the list of entries, and return an empty list in the empty case.

Tables of Tables

There are still some rough edges, but we are getting somewhere! Let’s tackle the next glaring problem with our approach, namely:

Ability (roll 1d12)
---
// omitted entries
8  MAGIC TYPE
// omitted entries

What the MAGIC TYPE entry means is, “when you roll a 8, pick from the table MAGIC TYPE”.

So the ABILITY table needs to know somehow about the MAGIC TYPE table. How do we do that?

One possible direction would be to embed that table directly in our expression, like this:

let ability = [
    Or [ "bless"; "curse" ]
    Or [
        Or [
            Item "divination"
            Item "enchantment"
            ]
        ]
    ]

However, that is starting to look unwieldy. Also, some tables can be called from multiple other tables, so rather than repeating these tables in a giant tree, we will assume that the picking takes place within a context, with named tables that we can re-use.

Let’s rework a bit our code:

type TableRef = | Ref of string

type Entry<'T> =
    | Item of 'T
    | And of list<Entry<'T>>
    | Or of list<Entry<'T>>
    | Table of TableRef

type NamedTable<'T> = {
    Name: string
    Entries: Distribution<Entry<'T>>
    }

type Context<'T> = {
    RNG: Random
    Tables: Map<TableRef, NamedTable<'T>>
    }

Armed with that reorganization, we can rewrite our eval function:

[<RequireQualifiedAccess>]
module Table =

    let eval ctx table =
        let rec eval (ctx: Context<'T>) (entry: Entry<'T>) =
            match entry with
            | Item item -> List.singleton item
            | And entries -> entries |> List.collect (eval ctx)
            | Or entries -> entries |> Pick.uniform ctx.RNG |> eval ctx
            | Table ref -> 
                ctx.Tables.[ref].Entries 
                |> Pick.from ctx.RNG 
                |> eval ctx
            |> List.distinct
        eval ctx (Table (Ref table))

… which we can use to run our example:

let ability = {
    Name = "ability"
    Entries =
        Uniform [
            Or [ Item "bless"; Item "curse"]
            Or [ Item "entangle"; Item "trap"; Item "ensnare" ]
            Table (Ref "magic type")
            // omitted entries
            ]
    }

let magicType = {
    Name = "magic type"
    Entries =
        Uniform [
            Item "divination"
            Item "enchantment"
            // omitted entries
            ]
    }

let ctx = {
    RNG = Random ()
    Tables = [
        ability
        magicType
        ]
        |> List.map (fun t -> Ref t.Name, t)
        |> Map.ofList
    Merge = fun (a, b) -> a + b
    }

> Table.eval ctx "ability";;
val it: string list = ["bless"]
> Table.eval ctx "magic type";;
val it: string list = ["divination"]

Note: there are some glaring issues with the design. First, ctx.Tables.[ref].Entries will crash if the table name does not exist. Then, we could introduce an infinite loop if there is a circular reference between tables. I will assume for now that tables are created without cycles.

Roll Twice

This one is a classic of tables! Let’s add that to our expressions, generalizing the idea:

type Entry<'T> =
    | Item of 'T
    // omitted code
    | Repeat of int * Entry<'T>

We can modify the eval function accordingly:

let rec eval (ctx: Context<'T>) (entry: Entry<'T>) =
    // omitted code
    | Repeat (n, entry) ->
        List.init n (fun _ -> entry |> eval ctx)
        |> List.collect id

Armed with this, we can now represent what we need:

let ability = {
    Name = "ability"
    Entries =
        Uniform [
            Or [ Item "bless"; Item "curse"]
            Or [ Item "entangle"; Item "trap"; Item "ensnare" ]
            Table (Ref "magic type")
            // omitted entries
            Repeat (2, Table (Ref "ability"))
            ]
    }

As a side note, this is why the eval function returns a list<'T>, and not just a 'T: picking from a list can return more than one item. For that matter, it could theoretically produce an infinite list of elements, if we happened to pick the Repeat entry over and over and over again.

As another side note, this also introduces the possibility of infinite loops. As a trivial example, the following table will never finish evaluating:

let ouroboros = { 
    Name = "ouroboros"
    Entries = Flat [ Repeat (2, Table (Ref "ouroboros")) ]
    }

The tricky case of Immunity to Element

Are we done? Almost! Our original sample table has one entry we do not quite handle yet:

Ability (roll 1d12)
---
// omitted entries
10 immunity: ELEMENT
11 read/control minds
12 roll twice on this table

I really struggled with immunity: ELEMENT. What it means is “when you roll a 10, roll on the ELEMENT table, and return immunity to the picked element”, for instance “immunity to Fire”.

What makes this case different is that we are not just picking a list of 'T’s, we are merging the result of the pick with something else. The way I approached this was by introducing a new case in our expressions,

type Entry<'T> =
    | Item of 'T
    // omitted code
    | Merge of (Entry<'T> * Entry<'T>)

In our specific example, the expression would be, for instance:

Merge (Item "immunity", Table (Ref "element"))

In the general case, evaluating the 2 entries will result in 2 lists, which we need to merge. What we want is the cross-product of the 2 evaluations, something along these lines:

| Merge (entry1, entry2) ->
    eval ctx entry1
    |> List.collect (fun value1 ->
        eval ctx entry2
        |> List.map (fun value2 ->
            // merge value1, a 'T and value2, a 'T
            // into a 'T
            merge (value1, value2)
            )
        )

So we need a function to merge 2 values of a given type, into 1 value of the same type, something with a signature along these lines:

('T * 'T) -> 'T

In our specific example, we can easily write such a function, we just need to combine 2 strings into 1, for instance like this:

let merge (txt1: string, txt2: string) = $"{txt1} {txt2}"

The question here is, where should this function live? Who knows how to merge “things”?

My initial train of thought was to make that a property of the “thing” itself, perhaps through an interface, say, IMergeable, perhaps through a Statically Resolved Type Parameter. After a few attempts in that direction, I backtracked. The code was getting unwieldy, and it felt a bit off. In the end, how you merge strings (for instance) is not a property of the string, it is context dependent.

What I landed on is making that function part of the Context:

type Context<'T> = {
    RNG: Random
    Tables: Map<TableRef, NamedTable<'T>>
    Merge: 'T * 'T -> 'T
    }

We can plug that right into our eval function:

| Merge (entry1, entry2) ->
    eval ctx entry1
    |> List.collect (fun value1 ->
        eval ctx entry2
        |> List.map (fun value2 ->
            ctx.Merge (value1, value2)
            )
        )

On the upside, it works. At the same time, something bugs me about this solution. Perhaps it is just a personal hang-up about making functions part of a Record, perhaps there is something more to it. In the back of my mind, I imagine somewhere there is a Category Theorist with a hint of a smile, thinking “what the poor man needs is a bifunctor coequalizer” (or something equally awesome sounding). I know next to nothing about the topic, but if you have thoughts on how to make this better (with or without Category Theory!), I am all ears :)

Parting words

First, I hope that you got something out of this meandering exploration of modeling random tables! As usual, what started out as a “surely, this will be a small weekend project” ended up being both more complex, and more interesting than what I anticipated.

If you are interested in the code, you can find the current state of affairs on GitHub. I plan to keep going at a leisurely pace, and at the moment I am interested in the following questions:

Incorporate dice rolls in Expressions, to support things like “roll 1d6 times on the treasure table”,
Compose complex entities from Tables, for instance, generating random monsters,
Render results in a web page using a generic template with Fable,
Potentially write parsers for tables,
Potentially explore conditional probabilities (change the distribution on a Table based on earlier rolls).

That’s what I have for today’s installment! In the meanwhile, may 2022 bring a lot of happy coding, and ping me on Twitter or leave a comment if you have thoughts or questions!

Do you have a comment or a question?
Ping me on Mastodon!