28 Dec 2024
During December, I have been aggressively redesigning my library, Quipu. I
initially wrote Quipu because I needed a Nelder-Mead solver in .NET, and
could not find one ready to use. And, because I intended to use it from F#,
I wrote Quipu in a style that wasn’t particularly C# friendly.
As I was going through the code base with my chainsaw, I thought it would be an
interesting exercise to try and make it pleasant to use from C# as well. This
post will go through some of the process.
First, what is Quipu about? Quipu is an implementation of the Nelder-Mead
algorithm, and searches for arguments that minimize a function. As an example,
suppose you were given the function f(x,y) = (x-1)^2 + (y-2)^2 + 42, and
wanted to know what values of x and y give you the lowest possible value
for f. With Quipu, now in C#, this is how you would go about it:
#r "nuget: Quipu, 0.5.2"
using Quipu.CSharp;
using System;
Func<Double,Double,Double> f =
(x, y) => Math.Pow(x - 1.0, 2) + Math.Pow(y - 2.0, 2) + 42.0;
var solverResult =
NelderMead
.Objective(f)
.Minimize();
if (solverResult.HasSolution)
{
var solution = solverResult.Solution;
Console.WriteLine($"Solution: {solution.Status}");
var candidate = solution.Candidate;
var args = candidate.Arguments;
var value = candidate.Value;
Console.WriteLine($"f({args[0]:N3}, {args[1]:N3}) = {value:N3}");
}
This produces the following result, which happens to be correct:
Solution: Optimal
f(1.000, 2.000) = 42.000
I would also like to think that this C# code looks reasonably pleasant, whereas
the original version (pre version 0.5.*) definitely was not. Let’s go over some
of the changes I made to the original code!
Side note: my C# is pretty rusty at that point, if you have any thoughts or
feedback on how to make this better, I am all ears!
More...
13 Oct 2024
Since my earlier post looking into SIMD vectors in .NET, I
attempted a few more experiments, trying to understand better where
they might be a good fit, and where they would not.
The short version: at that point, my sense is that SIMD vectors can be very
handy for some specific scenarios, but would require quite a bit of work to be
usable in the way I was hoping to use them. This statement is by no means meant
as a negative on SIMD; rather, it reflects my realization that a SIMD vector is
quite different from a mathematical vector.
All that follows should also be taken with a big grain of
salt. SIMD is entirely new to me, and I might not be using it
right. While on that topic, I also want to thank @xoofx for his
very helpful comments - much appreciated!
Anyways, with these caveats out of the way, let’s dive into it.
My premise approaching SIMD was along these lines: “I write a lot of code that
involves vectors. Surely, the Vector class should be a good fit to speed up
some of that code”.
To explore that idea, I attempted to write a few classic vector operations I
often need, both in plain old F# and using SIMD vectors, trying to benchmark
how much performance I would gain. In this post, I’ll share some of the
results, and what I learnt in the process.
You can find the whole code here on GitHub.
More...
01 Sep 2024
Even though a lot of my work involves writing computation-heavy code, I have
not been paying close attention to the System.Numerics namespace, mainly
because I am lazy and working with plain old arrays of floats has been good
enough for my purposes.
This post is intended as a first dive into the question “should I care about
.NET SIMD-accelerated types”. More specifically, I am interested in
understanding better Vector<T>, and in where I should use it instead of
basic arrays for vector operations, a staple of machine learning.
Spoiler alert: some of my initial results surprised me, and I don’t understand
yet what drives the speed differences between certain examples. My intent here
is to share what I found so far, which I found interesting enough to warrant
further exploration later on.
Anyways, let’s dive in. As a starting point, I decided to start with a very
common operation in Machine Learning, computing the Euclidean distance
between 2 vectors.
You can find the whole code here on GitHub.
More...
20 Apr 2024
The main reason I created Quipu is that I needed a Nelder-Mead solver for a
real-world project. And, as I put Quipu through its paces on real-world data,
I ran into some issues, revolving around “Not a Number” floating point values,
aka NaN.
tl;dr: the latest release of Quipu, version 0.2.2, available on
nuget, should handle NaN values decently well, and has some minor
performance improvements, too.
In this post, I will go over some of the changes I made, and why. Fixing the
main issue made me realize that I didn’t know floating point numbers as well as
I thought, even though I have been using them every working day for years. I
will take some tangents to discuss some of my learnings.
So let’s dig in. My goal with Quipu was to implement the
Nelder-Mead algorithm in F#. The purpose of Nelder-Mead is to find a
numeric approximation of values that minimize a function. As an illustration,
if we took the function $f(x) = x ^ 2$, we would like to know what value of $x$
produces the smallest possible value for $f(x)$, which happens to be $x = 0$ in
this case.
Quipu handles that case just fine:
open Quipu.NelderMead
let f x = x ** 2.0
f
|> NelderMead.minimize
|> NelderMead.solve
val it: Solution = Optimal (0.0, [|0.0|])
So far, so good. Now, what about a function like $f(x) = \sqrt{x}$?
That function is interesting for 2 reasons:
- $f(x)$ has a minimum, for $x = 0$.
- $f(x)$ is defined only for $x \ge 0$: it is a partial function.
Sadly, the previous version of Quipu, version 0.2.1, failed to find it. It
would go into an infinite loop instead.
More...
26 Feb 2024
An old math problem I had not seen since my university days resurfaced the other
day, the Maximum Flow problem. It came up in the context of analyzing
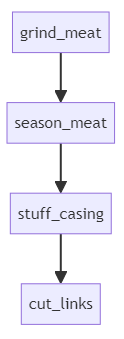
some industrial process. For illustration purposes, let’s say we are producing
sausages, following these steps: we grind some meat, add some seasoning, then
stuff and tie the sausage casings, and split them into delicious sausage links.
We could represent this process as a graph, like so:
``` mermaid
graph TD;
grind_meat --> season_meat;
season_meat --> stuff_casing;
stuff_casing --> cut_links;
Now the question is, how many sausages per minute could we produce?
Assuming each operation is performed by a separate person, this is not very
complicated. We are going to be as slow as the slowest link. So if for instance
we could
- grind meat for 20 sausages / minute,
- season meat for 15 sausages per minute,
- stuff 5 sausages per minute, and
- cut 20 sausages per minute,
we would end up running at 5 sausages / minute at best, the bottleneck being
stuffing.
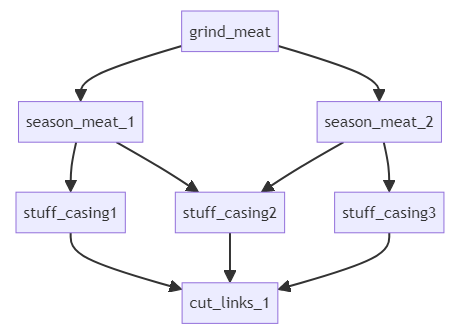
Now we might be able to get a better throughput with some parallelization. For
instance, we could organize production like so:
``` mermaid
graph TD;
grind_meat --> season_meat_1;
grind_meat --> season_meat_2;
season_meat_1 --> stuff_casing1;
season_meat_1 --> stuff_casing2;
season_meat_2 --> stuff_casing2;
season_meat_2 --> stuff_casing3;
stuff_casing1 --> cut_links_1;
stuff_casing2 --> cut_links_1;
stuff_casing3 --> cut_links_1;
This is still not overly complicated, but it is beginning to be hairy, and you
can imagine how with a few more processes added, the question “how much work
can I process through this network” will soon become impractical to handle by
hand.
This is essentially what the Maximum Flow problem is about. Given a directed
graph, with capacity limitations, how much throughput (flow) can we achieve?
In the rest of this post, I’ll go through one way you could answer that
question, using Linear Programming.
More...


